Line coding
Line coding refers to the process of converting digital data into digital signals. Whenever we transmit data it is in the form of digital signals, so with the help of line coding, we can convert a sequence to bits (or encoding) into a digital signal which then again converted into bits by the receiver (or can be said as decoded by the receiver). For all this to happen we need line coding schemes which could also be able to avoid overlapping and distortion of signals.
Some necessary characteristics of line coding schemes:
So in this article we are going to talk about three types of line coding schemes:
Let's get into the detail.
Unipolar Line Coding

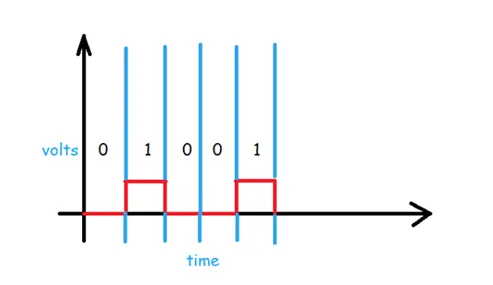
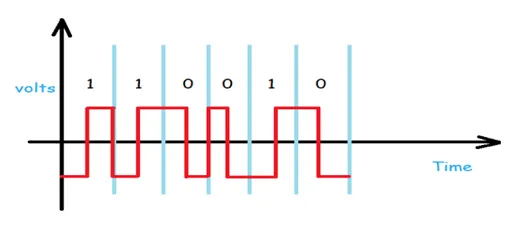
In Unipolar we are simply representing a signal in a graphical form where positive voltage represents logical or binary 1 and zero voltage represents logical zero. We can say that it's the simplest line code. The drawback of this scheme is that it is not self-clocking which means that it can't be decoded without a separate clock signal or any other synchronization source. And as we discussed in the characteristics section that there should be no DC component present which it significantly contains, which can be halved by returning to zero in the middle of the bit period.
NRZ (Non-Return to Zero):
The term Non-Return to Zero (NRZ) means that the signal (the red line in the above diagram) will not return to zero in middle of the bit (i.e. either 0 or 1). Unipolar schemes were generally designed as NRZ schemes. But if we compare it to the polar NRZ scheme, this scheme leads to wastage of power i.e. the normalized power (i.e. the power required to send 1-bit per resistance) is almost double as compared to polar NRZ.
Because of all these reasons unipolar encoding is not normally used in data communications today.
Polar Line Coding
As its name suggests polar which means it will have both positive and negative values for voltages or amplitude, it is quite like NRZ scheme but, here we have NRZ-L (i.e. NRZ-Level) and NRZ-I (i.e. NRZInvert).
Let's see how these are represented:
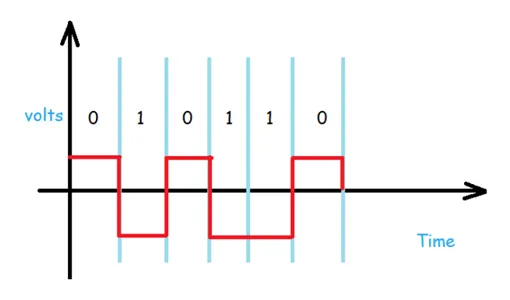
In the above diagram, we can simply notice that high volt is for logical 0 and low volt is for logical 1. This is the representation of NRZ-Level.
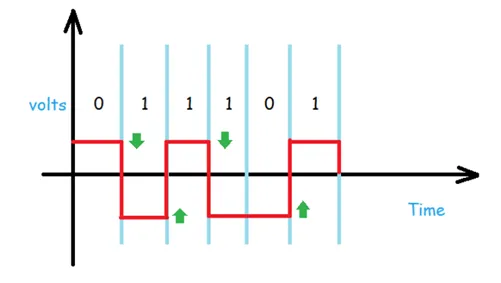
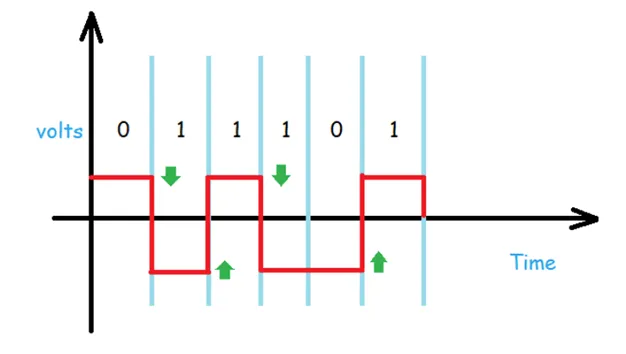
Now in this one, the idea is that whenever we encounter logical 1 then the signal will be inverted, but when it encounters logical 0 then it remains on the same side. This is the NRZ-Invert.
The Baseline wandering is a problem for both of them, but for NRZ-L it is twice as bad as compared to NRZ-I, because of the transition at the boundary for NRZ-I. similarly, the self-synchronization problem is similar in both for a long sequence of 0’s, but for a long sequence of 1’s, it is more severe in NRZ-L.
Return to Zero (RZ):
Return to zero proved out to be a nice alternative or say a solution to NRZ drawbacks. Unlike NRZ, RZ uses three values of voltage i.e. positive, negative, zero. And as the name suggests it returns to zero in the middle of each bit.
The idea behind the above representation is that logical 1 is represented as half-positive and half-zero volts and the logical 0 is represented as halfnegative and half-zero volts.
Now, this scheme also has some drawbacks which are as follows:
Requires a large bandwidth for transmission.
Complex encoding as it uses three levels of voltages
This scheme is not used nowadays and is replaced by Manchester encoding & Differential-Manchester encoding.
Manchester & Differential-Manchester Encoding:
We can say that Manchester encoding is a combination of RZ and NRZ-L. here, instead of using three values of voltages we use only two, here logical 1 is represented in two halves, the first half consists of a negative voltage and the second-half is represented as positive voltage, and logical 0 is also represented in two halves, the first half consists of a positive voltage and the second-half is represented as negative voltage. The transition in the middle of the bit provides synchronization.
The Differential-Manchester encoding can be said as the combination of RZ & NRZ-I. here, we use the same logic as we used in NRZ-I i.e. inversion will take place when we encounter logical 1 and if we encounter logical 0 then no inversion.
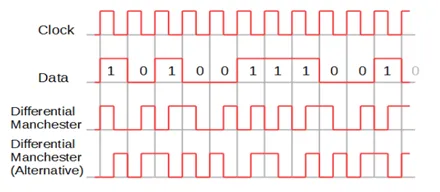
Manchester encoding had a huge impact since it was able the solution for several problems related to NRZ-L and on the other hand Differential Manchester overcome the problems associated with NRZ-I, since there is no baseline wandering and no low frequency component or DC component, because every logical bit was having positive and negative voltage contribution.
The area where Manchester encoding, and Differential Manchester encoding are limited is the bandwidth. The minimum bandwidth of Manchester encoding, and Differential Manchester encoding is twice as that of NRZ.
Bipolar Line Coding
Bipolar consists of three voltage levels which are positive negative and zero. While representing, the voltage level for one bit of data is at zero, and the other bit inverts of transits or alternates between positive and negative voltage.
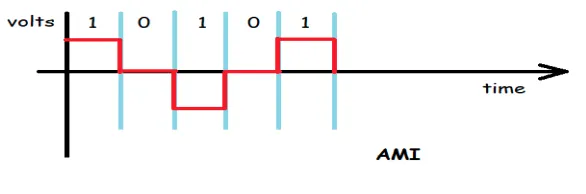
ALTERNATE MARK INVERSION(AMI): the representation here follows a simple logic that is, for representing logical 0 we use zero voltage, and while representing logical 1 we use alternating positive and negative voltages, which can be seen in the image below.
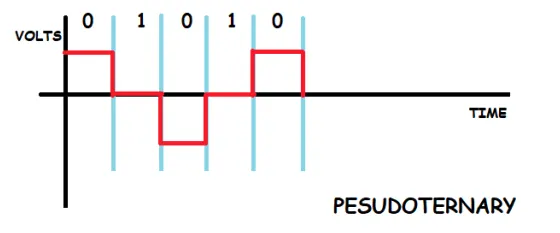
Pesudoternary: this is the opposite of AMI, as we kept logical 0 at 0 volts or neutral in the above section, here we will be keeping logical 1 as neutral (i.e. at 0 volts) and we will keep alternating logical zero, we can see that in the image below.
The bipolar scheme or encoding proved to be an alternative for NRZ encoding because bipolar has the same signal rate as NRZ, and also it was not having any low frequency or DC component in it, as one bit is represented by zero volts and the other is represented by alternating voltages.