Exponential Backoff Algorithm

Whenever there is a collision the exponential backoff algorithm – operating at the MAC layer – is used to determine when each station will retry its transmission. Backoff here is called exponential because the range from which the backoff value is chosen is doubled after every successive collision involving the same packet. Here is the full Ethernet transmission algorithm, including backoff and retransmissions:

1.      Listen before transmitting (“carrier detect”)

2.      If line is busy, wait for sender to stop and then wait an additional 9.6 microseconds (96 bits). One consequence of this is that there is always a 96-bit gap between packets, so packets do not run together.

3.      Transmit while simultaneously monitoring for collisions

4.      If a collision does occur, send the jam signal, and choose a backoff time as follows: For transmission N, 1≤N≤10 (N=0 represents the original attempt), choose k randomly with 0 ≤k ≤2^N. Wait k slot times (k x 51.2 µsec). Then check if the line is idle, waiting if necessary for someone else to finish, and then retry step 3. For 11≤N≤15, choose k randomly with 0 ≤ k < 1024 (= 2¹⁰)

5.      If we reach N=16 (16 transmission attempts), give up.

If an Ethernet sender does not reach step 5, there is a very high probability that the packet was delivered successfully

Exponential backoff means that if two hosts have waited for a third to finish and transmit simultaneously, and collide, then when N=1 they have a 50% chance of recollision; when N=2 there is a 25% chance, etc. When N≥10 the maximum wait is 52 milliseconds; without this cutoff the maximum wait at N=15 would be 1.5 seconds. As indicated above in the minimum-packet-size discussion, this retransmission strategy assumes that the sender is able to detect the collision while it is still sending, so it knows that the packet must be resent.

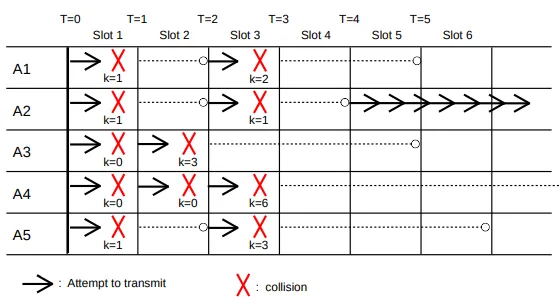
In the following diagram is an example of several stations attempting to transmit all at once, and using the above transmission/backoff algorithm to sort out who actually gets to acquire the channel. We assume we have five prospective senders A1, A2, A3, A4 and A5, all waiting for a sixth station to finish. We will assume that collision detection always takes one slot time (it will take much less for nodes closer together) and that the slot start-times for each station are synchronized; this allows us to measure time in slots. A solid arrow at the start of a slot means that sender began transmission in that slot; a red X signifies a collision. If a collision occurs, the backoff value k is shown underneath. A dashed line shows the station waiting k slots for its next attempt.

At T=0 we assume the transmitting station finishes, and all the Ai transmit and collide. At T=1, then, each of the Ai has discovered the collision; each chooses a random k<2. Let us assume that A1 chooses k=1, A2 chooses k=1, A3 chooses k=0, A4 chooses k=0, and A5 chooses k=1.><2. Let us assume that A1 chooses k=1, A2 chooses k=1, A3 chooses k=0, A4 chooses k=0, and A5 chooses k=1.

Those stations choosing k=0 will retransmit immediately, at T=1. This means A3 and A4 collide again, and at T=2 they now choose random k<4. We will Assume A3 chooses k=3 and A4 chooses k=0; A3 will try again at T=2+3=5 while A4 will try again at T=2, that is, now><4. We will Assume A3 chooses k=3 and A4 chooses k=0; A3 will try again at T=2+3=5 while A4 will try again at T=2, that is, now.

At T=2, we now have the original A1, A2, and A5 transmitting for the second time, while A4 trying again for the third time. They collide. Let us suppose A1 chooses k=2, A2 chooses k=1, A5 chooses k=3, and A4 chooses k=6 (A4 is choosing k<8 at random). Their scheduled transmission attempt times are now A1 at T=3+2=5, A2 at T=4, A5 at T=6, and A4 at T=9.><8 at random). Their scheduled transmission attempt times are now A1 at T=3+2=5, A2 at T=4, A5 at T=6, and A4 at T=9.

At T=3, nobody attempts to transmit. But at T=4, A2 is the only station to transmit, and so successfully seizes the channel. By the time T=5 rolls around, A1 and A3 will check the channel, that is, listen first, and wait for A2 to finish. At T=9, A4 will check the channel again, and also begin waiting for A2 to finish.

A maximum of 1024 hosts is allowed on an Ethernet. This number apparently comes from the maximum range for the backoff time as 0≤k≤ 1024. If there are 1024 hosts simultaneously trying to send, then, once the backoff range has reached k<1024 (N=10), we have a good chance that one station will succeed in seizing the channel, that is; the minimum value of all the random k’s chosen will be unique><1024 (N=10), we have a good chance that one station will succeed in seizing the channel, that is; the minimum value of all the random k’s chosen will be unique.

This backoff algorithm is not “fair”, in the sense that the longer a station has been waiting to send, the lower its priority sinks. Newly transmitting stations with N=0 need not delay at all. The Ethernet capture effect, below, illustrates this unfairness.