Work and Energy Kinetics – Velocity and acceleration

Work Transfers Energy

What happens to the work done on a system? Energy is transferred into the system, but in what form? Does it remain in the system or move on? The answers depend on the situation. For example, if the lawn mower in Figure 7.2(a) is pushed just hard enough to keep it going at a constant speed, then energy put into the mower by the person is removed continuously by friction, and eventually leaves the system in the form of heat transfer. In contrast, work done on the briefcase by the person carrying it up stairs in Figure 7.2(d) is stored in the briefcase-Earth system and can be recovered at any time, as shown in Figure 7.2(e). In fact, the building of the pyramids in ancient Egypt is an example of storing energy in a system by doing work on the system. Some of the energy imparted to the stone blocks in lifting them during construction of the pyramids remains in the stone-Earth system and has the potential to do work.

In this section we begin the study of various types of work and forms of energy. We will find that some types of work leave the energy of a system constant, for example, whereas others change the system in some way, such as making it move. We will also develop definitions of important forms of energy, such as the energy of motion.

Net Work and the Work-Energy Theorem

We know from the study of Newton’s laws in Dynamics: Force and Newton's Laws of Motion that net force causes acceleration. We will see in this section that work done by the net force gives a system energy of motion, and in the process we will also find an expression for the energy of motion.

Let us start by considering the total, or net, work done on a system. Net work is defined to be the sum of work done by all external forces—that is, net work is the work done by the net external force Fnetsize 12{F rSub { size 8{"net"} } } {}. In equation form, this is Wnet=Fnetdcosθsize 12{W rSub { size 8{"net"} } =F rSub { size 8{"net"} } d"cos"θ} {} where θsize 12{θ} {} is the angle between the force vector and the displacement vector.

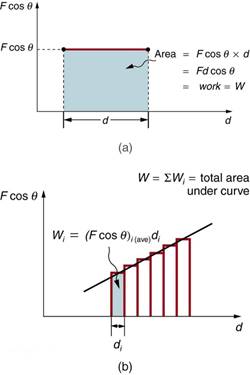
Figure 7.3(a) shows a graph of force versus displacement for the component of the force in the direction of the displacement—that is, an Fcosθsize 12{F"cos"θ} {} vs. dsize 12{d} {} graph. In this case, Fcosθsize 12{F"cos"θ} {} is constant. You can see that the area under the graph is Fdcosθsize 12{F"cos"θ} {}, or the work done. Figure 7.3(b) shows a more general process where the force varies. The area under the curve is divided into strips, each having an average force (Fcosθ)i(ave)size 12{ \( F"cos"θ \) rSub { size 8{i \( "ave" \) } } } {}. The work done is (Fcosθ)i(ave)disize 12{ \( F"cos"θ \) rSub { size 8{i \( "ave" \) } } d rSub { size 8{i} } } {} for each strip, and the total work done is the sum of the Wisize 12{W rSub { size 8{i} } } {}. Thus the total work done is the total area under the curve, a useful property to which we shall refer later.

Figure 7.3 (a) A graph of Fcosθ vs. dsize 12{d} {}, when Fcosθsize 12{F"cos"θ} {} is constant. The area under the curve represents the work done by the force. (b) A graph of Fcosθsize 12{F"cos"q} {} vs. dsize 12{d} {} in which the force varies. The work done for each interval is the area of each strip; thus, the total area under the curve equals the total work done.

Net work will be simpler to examine if we consider a one-dimensional situation where a force is used to accelerate an object in a direction parallel to its initial velocity. Such a situation occurs for the package on the roller belt conveyor system shown in Figure 7.4.

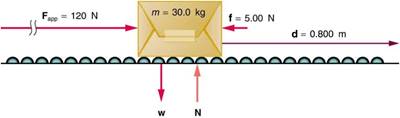
Figure 7.4 A package on a roller belt is pushed horizontally through a distance d.