Mathematical Modeling definition

Mathematical Modeling and the Scientific Method

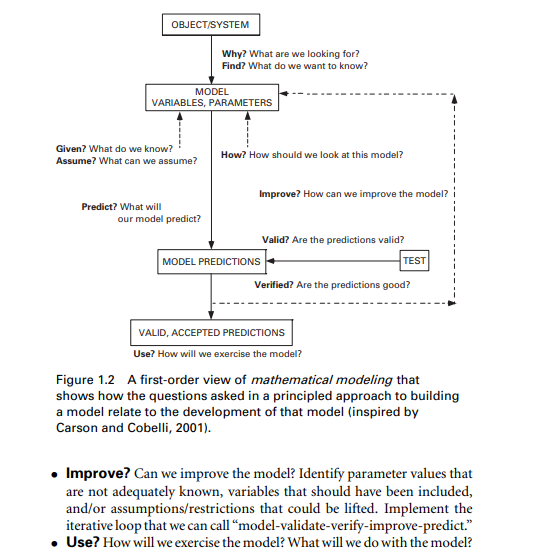
Why Do We Do Mathematical Modeling?

Some Methods of Mathematical Modeling

conservation and balance principles, and consequences of linearity. We will expand these themes more extensively in the first part of this book.

Dimensional Homogeneityand Consistency

There is a basic, yet very powerful idea that is central to mathematical modeling, namely, that every equation we use must be dimensionally homogeneous or dimensionally consistent. It is quite logical that every term in an energy equation has total dimensions of energy, and that every term in a balance of mass should have the dimensions of mass. This statement provides the basis for a technique called dimensional analysis that we will discuss in greater detail in Chapter 2. In that discussion we will also review the important distinction between physical dimensions that relate a (derived) quantity to fundamental physical quantities and units that are numerical expressions of a quantity’s dimensions expressed in terms of a given physical standard.

Abstraction and Scaling

An important decision in modeling is choosing an appropriate level of detail for the problem at hand, and thus knowing what level of detail is prescribed for the attendant model. This process is called abstraction and it typically requires a thoughtful approach to identifying those phenomena on which we want to focus, that is, to answering the fundamental question about why a model is being sought or developed.

For example, a linear elastic spring can be used to model more than just the relation between force and relative extension of a simple coiled spring, as in an old-fashioned butcher’s scale or an automobile spring. It can also be used to model the static and dynamic behavior of a tall building, perhaps to model wind loading, perhaps as part of analyzing how the building would respond to an earthquake. In these examples, we can use a very abstract model by subsuming various details within the parameters of that model. We will explore these issues further in Chapter 3.

In addition, as we talk about finding the right level of abstraction or the right level of detail, we are simultaneously talking about finding the right scale for the model we are developing. For example, the spring can be used at a much smaller, micro scale to model atomic bonds, in contrast with the macro level for buildings. The notion of scaling includes several ideas, including the effects of geometry on scale, the relationship of function to scale, and the role of size in determining limits—all of which are needed to choose the right scale for a model in relation to the “reality” we want to capture.

Conservation and Balance Principles

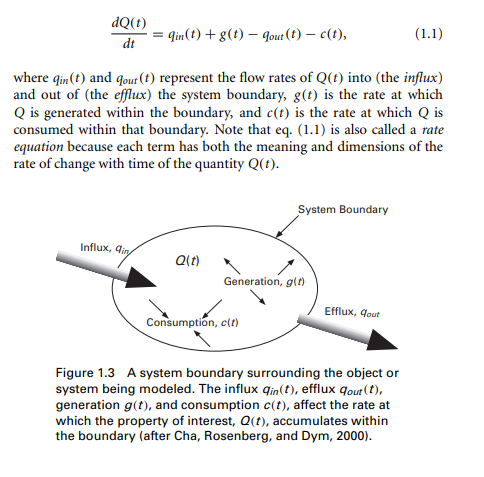
When we develop mathematical models, we often start with statements that indicate that some property of an object or system is being conserved. For example, we could analyze the motion of a body moving on an ideal, frictionless path by noting that its energy is conserved. Sometimes, as when we model the population of an animal colony or the volume of a river flow, we must balance quantities, of individual animals or water volumes, that cross a defined boundary. We will apply balance or conservation principles to assess the effect of maintaining or conserving levels of important physical properties. Conservation and balance equations are related—in fact, conservation laws are special cases of balance laws. The mathematics of balance and conservation laws are straightforward at this level of abstraction. Denoting the physical property being monitored as Q(t) and the independent variable time as t, we can write a balance law for the temporal or time rate of change of that property within the system boundary depicted in Figure 1.3 as:

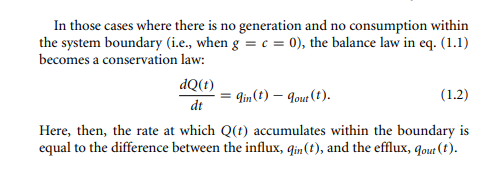
Constructing Linear Models

Linearity is one of the most important concepts in mathematical modeling. Models of devices or systems are said to be linear when their basic equations—whether algebraic, differential, or integral—are such that the magnitude of their behavior or response produced is directly proportional to the excitation or input that drives them. Even when devices like the pendulum discussed in Chapter 7 are more fully described by nonlinear models, their behavior can often be approximated by linearized or perturbed models, in which cases the mathematics of linear systems can be successfully applied. We apply linearity when we model the behavior of a device or system that is forced or pushed by a complex set of inputs or excitations. We obtain the response of that device or system to the sum of the individual inputs by adding or superposing the separate responses of the system to each individual input. This important result is called the principle of superposition. Engineers use this principle to predict the response of a system to a complicated input by decomposing or breaking down that input into a set of simpler inputs that produce known system responses or behaviors.