And-Or Graphs

Useful for certain problems where

• The solution involves decomposing the problem into smaller problems.
• We then solve these smaller problems.

Here the alternatives often involve branches where some or all must be satisfied before we can progress.

For example if I want to learn to play a Frank Zappa guitar solo I could (Fig. 2.2.1)

• Transcribe it from the CD. OR
• Buy the ``Frank Zappa Guitar Book'' AND Read it from there.

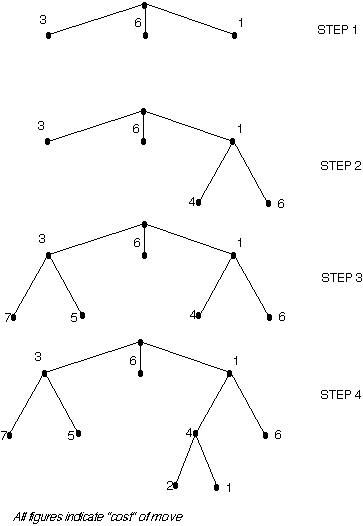
Note the use of arcs to indicate that one or more nodes must all be satisfied before the parent node is achieved. To find solutions using an And-Or GRAPH the best first algorithm is used as a basis with a modification to handle the set of nodes linked by the AND factor.

Inadequate: CANNOT deal with AND bit well.

AO* Algorithm

1. Initialise the graph to start node
2. Traverse the graph following the current path accumulating nodes that have not yet been expanded or solved
3. Pick any of these nodes and expand it and if it has no successors call this value FUTILITY otherwise calculate only f' for each of the successors.
4. If f' is 0 then mark the node as SOLVED
5. Change the value of f' for the newly created node to reflect its successors by back propagation.
6. Wherever possible use the most promising routes and if a node is marked as SOLVED then mark the parent node as SOLVED.
7. If starting node is SOLVED or value greater than FUTILITY, stop, else repeat from 2.