
A possible cause of frustration when using cross-entropy with classification problems with a large number of labels is the one hot encoding process.
For example, predicting words in a vocabulary may have tens or hundreds of thousands of categories, one for each label. This can mean that the target element of each training example may require a one hot encoded vector with tens or hundreds of thousands of zero values, requiring significant memory.
Sparse cross-entropy addresses this by performing the same cross-entropy calculation of error, without requiring that the target variable be one hot encoded prior to training.
Sparse cross-entropy can be used in keras for multi-class classification by using ‘sparse_categorical_crossentropy‘ when calling the compile() function.

1 | model.compile(loss='sparse_categorical_crossentropy', optimizer=opt, metrics=['accuracy']) |
The function requires that the output layer is configured with an n nodes (one for each class), in this case three nodes, and a ‘softmax‘ activation in order to predict the probability for each class.

1 | model.add(Dense(3, activation='softmax')) |
No one hot encoding of the target variable is required, a benefit of this loss function.
The complete example of training an MLP with sparse cross-entropy on the blobs multi-class classification problem is listed below.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 | # mlp for the blobs multi-class classification problem with sparse cross-entropy loss from sklearn.datasets.samples_generator import make_blobs from keras.layers import Dense from keras.models import Sequential from keras.optimizers import SGD from matplotlib import pyplot # generate 2d classification dataset X, y = make_blobs(n_samples=1000, centers=3, n_features=2, cluster_std=2, random_state=2) # split into train and test n_train = 500 trainX, testX = X[:n_train, :], X[n_train:, :] trainy, testy = y[:n_train], y[n_train:] # define model model = Sequential() model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform')) model.add(Dense(3, activation='softmax')) # compile model opt = SGD(lr=0.01, momentum=0.9) model.compile(loss='sparse_categorical_crossentropy', optimizer=opt, metrics=['accuracy']) # fit model history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=100, verbose=0) # evaluate the model _, train_acc = model.evaluate(trainX, trainy, verbose=0) _, test_acc = model.evaluate(testX, testy, verbose=0) print('Train: %.3f, Test: %.3f' % (train_acc, test_acc)) # plot loss during training pyplot.subplot(211) pyplot.title('Loss') pyplot.plot(history.history['loss'], label='train') pyplot.plot(history.history['val_loss'], label='test') pyplot.legend() # plot accuracy during training pyplot.subplot(212) pyplot.title('Accuracy') pyplot.plot(history.history['acc'], label='train') pyplot.plot(history.history['val_acc'], label='test') pyplot.legend() pyplot.show() |
Running the example first prints the classification accuracy for the model on the train and test dataset.
Given the stochastic nature of the training algorithm, your specific results may vary. Try running the example a few times.
In this case, we can see the model achieves good performance on the problem. In fact, if you repeat the experiment many times, the average performance of sparse and non-sparse cross-entropy should be comparable.

1 | Train: 0.832, Test: 0.818 |
A figure is also created showing two line plots, the top with the sparse cross-entropy loss over epochs for the train (blue) and test (orange) dataset, and the bottom plot showing classification accuracy over epochs.
In this case, the plot shows good convergence of the model over training with regard to loss and classification accuracy.
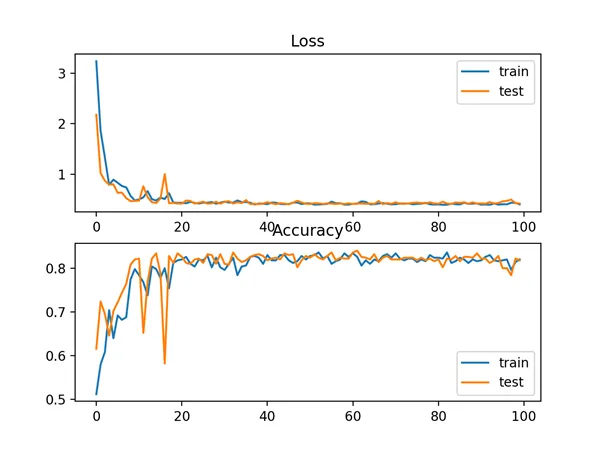
Line Plots of Sparse Cross Entropy Loss and Classification Accuracy over Training Epochs on the Blobs Multi-Class Classification Problem