SLIDER CRANK MECHANISM ANALYSIS BY RELATIVE VELOCITY METHOD

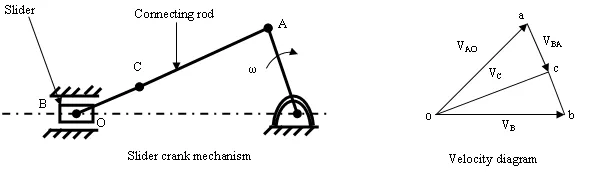
Angular velocity of link OA is given ω and velocity of point A can be given by, V_a = ω×OA = V_AO in the clockwise direction about O. V_ais perpendicular to OA. So we know the direction and magnitude of V_a. The velocity of slider B is along OB. The configuration and velocity diagram for this problem is given below.

Fig. 3.5

Step 1. Take any point o and draw vector oa such that oa= ω × OA=V_AO, perpendicular to OA in some suitable scale as shown in the velocity diagram.

Step 2. The velocity of point B with respect to A (V_BA) is perpendicular to AB. From a draw a vector ab perpendicular to the line AB.

Step 3. The velocity of slider B is along the line of stroke OB, from o draw a line parallel to OB which will intersect vector ab at b. The vector obrepresent the velocity of slider B (V_B).

The velocity of any point C on the connecting rod can be determined by the help of relation:

\[\frac{{{\mathbf{ac}}}}{{{\mathbf{ab}}}} = \frac{{{\text{AC}}}}{{{\text{AB}}}}{\text{ or }}{\mathbf{ac}} = {\mathbf{ab}} \times \frac{{{\text{AC}}}}{{{\text{AB}}}}\]                            

The point c can be located on the velocity diagram. Join o with c. vector oc represents the absolute velocity of point C with respect to O.

Example 3.1 In the mechanism as shown below, the crank O₂A rotates at 600 r.p.m. in the anticlockwise direction. The length of link O₂A= 12 cm and of link O₁B= 60 cm. Find

a. Angular velocity of link O₁A.

b. Velocity of slider at B.

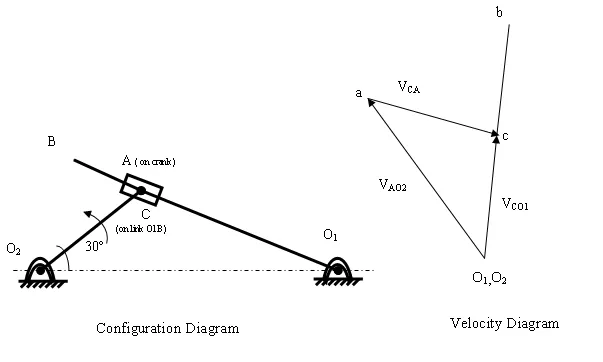
Fig. 3.6

Solution:   

Given:                  N=600 r.p.m

\[\omega={\text{ }}\frac{{{\text{2}}\pi{\text{N}}}}{{{\text{6}}0}} = \frac{{{\text{2}}\pi\times {\text{6}}00}}{{{\text{6}}0}} = {\text{2}}0{\text{ }}\pi {\text{ rad}}/{\text{sec}}\]                            

The velocity of A with respect to O₂

\[{{\text{V}}_{{\text{AO2}}}}= \omega\times{{\text{O}}_{\text{2}}}{\text{A}}={\text{2}}0\pi\times \frac{{{\text{12}}}}{{{\text{1}}00}} = {\text{7}}.{\text{53 m}}/{\text{s}}\]                            

In the configuration diagram let us take a point C on the link O₁B. The velocity diagram can be drawn as explain below.

Step 1. O₁ and O₂ are fixed points on the configuration diagram so they are taken as single point (o_1,o₂) on the velocity diagram. The velocity of point A with respect to O₂, V_AO2 = 7.53 m/s is drawn as vector o₂a in some suitable scale perpendicular to O₂A.

Step 2. The velocity of point C with respect to A, V_CA along the path of slider, O₁B. From a draw a vector ac representing V_CA   along O₁A. This will contain point c.

Step 3. The velocity of point C with respect to O₁ is V_CO1 and it will be perpendicular to O₁A.Then from o₁ draw a vector o₁c representing V_CO1this will intersect ac at point c.

Step 4. Locate the point b corresponding to point B such that

\[\frac{{{{\mathbf{o}}_{\mathbf{1}}}{\mathbf{b}}}}{{{{\mathbf{o}}_{\mathbf{1}}}{\mathbf{c}}}} =\frac{{{{\text{O}}_{\text{1}}}{\text{B}}}}{{{{\text{O}}_{\text{1}}}{\text{C}}}}\]

o₁b= 5.55 m/s by measurement

o₁b=V_BO1

Angular velocity of link O₁A

\[{\omega_{{\text{O1A}}}}={\omega _{{\text{O1B}}}}=\frac{{{{\text{V}}_{{\text{BO1}}}}}}{{{{\text{O}}_{\text{1}}}{\text{B}}}}= \frac{{{\text{5}}.{\text{55}}}}{{0.{\text{6}}0}}\]

= 9.25 rad/sec  

(anticlockwise direction)