APPLICATIONS OF SIMPLE HARMONIC MOTION
OBJECTIVES:
- Analyze the motion of a body to determine if it can be described either exactly or approximately in terms of simple harmonic motion and identify the conditions under which approximations to simple harmonic motion are valid.
- Use given information concerning simple mechanical systems, together with Newton's second law and/or conservation of energy, to solve for any of the kinematic or dynamic variables of simple harmonic motion.
PREREQUISITES:
Defining angular velocity, acceleration, displacement, and torque Applying Newton's second law for rotation to solve simple problems
Commentary:
Using the equations:
F(x) = -kx, (1)
m (d2x/dt2) = -kx. (2)
we will outline a method for analyzing a mechanical system to determine whether it can be characterized by simple harmonic motion.
- Determine the net force acting on the particle.
- Identify forces acting on the particle by drawing a free-body diagram. Choose a convenient coordinate system.
- Find the net force acting on the particle as a function of its position in the chosen coordinate system.
- Describe the particle's displacement from the equilibrium position.
- Find the position where the net force is equal to zero; this is the equilibrium position of the particle.
- If necessary, introduce a new coordinate system with its origin at the equilibrium position.
- Use the coordinate system introduced in II(b) to state Eqs. (1) and (2).
- Express the net force as a function of the new coordinates. Compare this with Eq. (1).
- Express the acceleration in terms of the second time derivative of the new coordinates.
- Use the expressions derived in steps (a) and (b) to state Newton's second law (F = ma) in terms of the new coordinates. Compare its form with Eq. (2).
Problem:
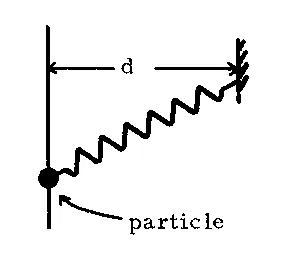
- A particle of mass m is constrained to move on a vertical frictionless track. It is attached to one end of the massless spring with spring constant k and unextended length l0 = 0 m (small compared to other lengths in the problem). The other end of the spring is hooked to a peg at the distance d from the track as shown in the diagram. See Figure.
- Show that the particle carries out simple harmonic motion when displaced from its equilibrium position.
- Find the period of oscillation of the particle.
Many systems that are actually rotational rather than rectilinear can be analyzed in terms of simple harmonic motion through the use of the small-angle approximation:
sin 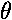

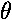 .
.
The first thing to note is that this is true only if 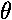 is in radians. Obviously sin 2.00° isn't 2. But 1° = 0.0174 rad, and sin(0.0349 rad) = 0.0348995 . This approximation is good up to about 15.0° or 0.262 rad where we have sin (0.262 rad) = 0.258. This is an error of only about 1%, so the approximation is pretty good; the error in the period of a pendulum when the amplitude is 15.0° is only 0.50%. Thus, even though a system actually does not execute simple harmonic motion, if the angular displacement is kept small enough its motion will be essentially simple harmonic. The listing below summarizes a few of the many common examples of simple harmonic oscillators along with the expressions for Fx or t. You should verify these expressions for yourself. The determination of
is in radians. Obviously sin 2.00° isn't 2. But 1° = 0.0174 rad, and sin(0.0349 rad) = 0.0348995 . This approximation is good up to about 15.0° or 0.262 rad where we have sin (0.262 rad) = 0.258. This is an error of only about 1%, so the approximation is pretty good; the error in the period of a pendulum when the amplitude is 15.0° is only 0.50%. Thus, even though a system actually does not execute simple harmonic motion, if the angular displacement is kept small enough its motion will be essentially simple harmonic. The listing below summarizes a few of the many common examples of simple harmonic oscillators along with the expressions for Fx or t. You should verify these expressions for yourself. The determination of 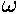 , f, and T for each system is left to you as an exercise.
, f, and T for each system is left to you as an exercise.
- Object on a spring: equilibrium occurs at the height for which the spring force equals mg. When the object is displaced from equilibrium, the spring force changes, the weight remains the same, the net restoring force is Fx = -k
 x.
x.
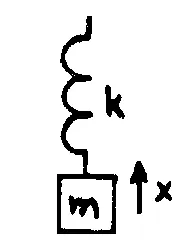
- Object fastened to two stretched springs: when the object is displaced, one spring pulls more, and the other pulls less. Restoring force is Fx = -(2k)x.
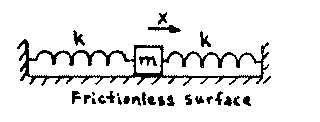
- Object fastened to two stretched springs, but displaced sideways: if the displacement is small, the forces exerted by the springs change in direction, but hardly at all in magnitude; the "spring" forces could also be exerted by elastic strings or some other medium obeying Hooke's law. Restoring force is
Fx = -2F0 (x/l).
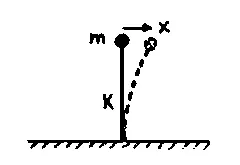
- Massive object on a "massless flagpole": for small displacement, the motion is almost linear. Restoring force is Fx = -Kx
- Object on a string (simple pendulum): the restoring force is the component of mg perpendicular to the string, -mg sin
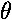 . For small displacements, the motion is almost linear, and sin
. For small displacements, the motion is almost linear, and sin 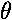

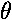 . Restoring force is
. Restoring force is
Fx = -mg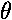 = -mg(x/l).
= -mg(x/l).
- Small object sliding in a frictionless spherical bowl: same as the simple pendulum. Restoring force is Fx = -mg
 . Or, use the restoring torque:
. Or, use the restoring torque:
 = -mgl
= -mgl with I = l2m and
with I = l2m and 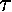 = I
= I = I d2
= I d2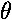 /dt2.
/dt2.

- Pivoted plank on spring: same as a car with good shocks in front, very bad shocks in back. As the object bounces up and down, the force of gravity is constant, but the spring force changes. Restoring torque is:
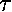 = - lk·l
= - lk·l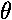 = -k l2
= -k l2 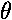
- Object hung from wire and rotating about a vertical axis (torsion pendulum); some mantlepiece clocks use a pendulum of this kind. Generally, the wire provides a restoring torque
 = -k
= -k
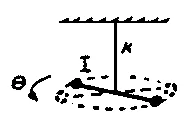
Although many pendulums are designed to approximate the simple pendulum by having their mass concentrated at the end of a string or rod, a more general case is that of the compound pendulum or physical pendulum as illustrated in the figure below:
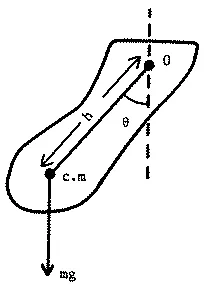
A compound pendulum consists of a rigid body of mass m suspended from an axis 0. The center of mass is a distance h from the axis. The torque about the axis 0 on the body is equal to the moment of inertia about the axis, I, times the angular acceleration:
 = I
= I = I(d2
= I(d2 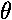 /dt2).
/dt2).
The restoring torque is provided by the weight mg:
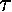 = -mgh sin
= -mgh sin 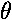 .
.
Therefore,
-mgh sin 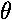 = I(d2
= I(d2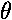 /dt2).
/dt2).
If 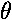 is small, sin
is small, sin 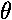

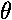 and
and
-mgh 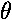 = I(d2
= I(d2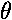 /dt2),
/dt2),
which is an equation for simple harmonic motion in terms of rotational variables.


![]()
![]()
![]() .
.![]() is in radians. Obviously sin 2.00° isn't 2. But 1° = 0.0174 rad, and sin(0.0349 rad) = 0.0348995 . This approximation is good up to about 15.0° or 0.262 rad where we have sin (0.262 rad) = 0.258. This is an error of only about 1%, so the approximation is pretty good; the error in the period of a pendulum when the amplitude is 15.0° is only 0.50%. Thus, even though a system actually does not execute simple harmonic motion, if the angular displacement is kept small enough its motion will be essentially simple harmonic. The listing below summarizes a few of the many common examples of simple harmonic oscillators along with the expressions for Fx or t. You should verify these expressions for yourself. The determination of
is in radians. Obviously sin 2.00° isn't 2. But 1° = 0.0174 rad, and sin(0.0349 rad) = 0.0348995 . This approximation is good up to about 15.0° or 0.262 rad where we have sin (0.262 rad) = 0.258. This is an error of only about 1%, so the approximation is pretty good; the error in the period of a pendulum when the amplitude is 15.0° is only 0.50%. Thus, even though a system actually does not execute simple harmonic motion, if the angular displacement is kept small enough its motion will be essentially simple harmonic. The listing below summarizes a few of the many common examples of simple harmonic oscillators along with the expressions for Fx or t. You should verify these expressions for yourself. The determination of ![]() , f, and T for each system is left to you as an exercise.
, f, and T for each system is left to you as an exercise.



![]() = -mg(x/l).
= -mg(x/l).
![]() = -mgl
= -mgl![]() with I = l2m and
with I = l2m and ![]() = I
= I![]() = I d2
= I d2![]() /dt2.
/dt2.
![]() = - lk·l
= - lk·l![]() = -k l2
= -k l2 ![]()



![]() = I
= I![]() = I(d2
= I(d2 ![]() /dt2).
/dt2).![]() = -mgh sin
= -mgh sin ![]() .
.![]() = I(d2
= I(d2![]() /dt2).
/dt2).![]() is small, sin
is small, sin ![]()
![]()
![]() and
and![]() = I(d2
= I(d2![]() /dt2),
/dt2),