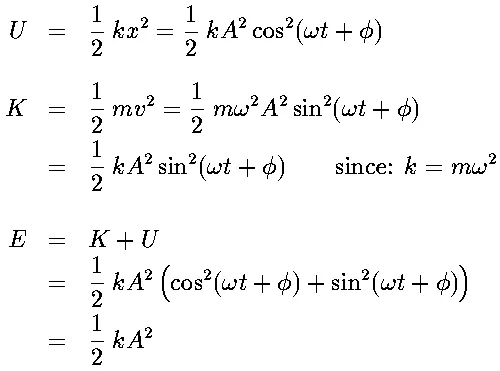
ENERGY CONSIDERATIONS IN SIMPLE HARMONIC MOTION

OBJECTIVE:

• Use conservation of energy and the equation for simple harmonic motion to analyze the relation between the kinetic and potential energy of a simple harmonic oscillator.

PREREQUISITES:

Defining potential and kinetic energy and identifying systems to which the principle of conservation of total mechanical energy may be applied

Commentary:

Harmonic motion can be analyzed in terms of a particle with a fixed total energy oscillating in a potential-energy "well," i.e., in the presence of a potential that increases in either direction away from the equilibrium point. In fact, this approach was used in the text in the initial development of the concept of the restoring force. Now that we have derived a general solution to the equation of simple harmonic motion and can write expressions for displacement and velocity as functions of time, we are in a position to verify that the sum of kinetic and potential energy is, in fact, constant for a simple harmonic oscillator.

Find equations in a textbook on the InfoMall that express the potential and kinetic energy of simple harmonic motion as functions of time:

Enter those equations here:

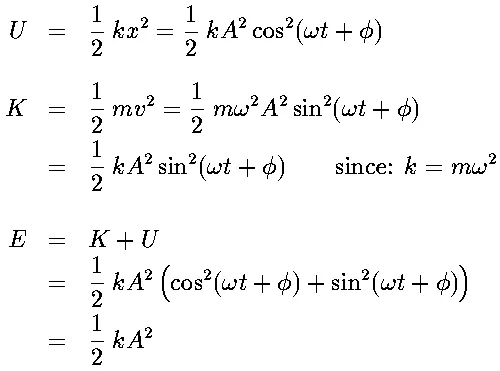
By applying the identity:

sin² + cos² = 1,

we find total energy is constant and equal to (1/2)kA².

This leads to several other useful results, such as an equation expressing velocity as a function of position, find or derive such an equation and enter it here:

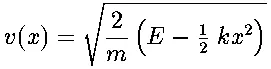
Finally the equation:

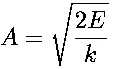
relates the amplitude of the SHM to the total energy. It can be used to find the amplitude of the motion if the total energy is known and vice versa.

Problem:

• For the oscillating particle described in Problem 2, what is the linear speed as a function of position?
• A 1.0-kg block rests on a frictionless table and is attached to a spring with a force constant of 250 N/m. The object is displaced 20 cm and given an initial velocity of 3 m/s away from the equilibrium position.
  1. What is the total energy of the resulting motion?
  2. What is the frequency of the motion?
  3. What is the amplitude of the motion?