SIMPLE HARMONIC MOTION AND UNIFORM CIRCULAR MOTION

OBJECTIVE:

• Describe simple harmonic motion as the projection of uniform circular motion along a diameter of the circle, and use the resulting analogy to analyze problems involving linear oscillations.

Commentary:

Viewed edge-on (i.e., projected along a diameter) the motion of a particle moving uniformly with angular speed  in a circle of radius A is indistinguishable from a particle oscillating harmonically in one dimension with amplitude A and angular frequency . This fact can be very useful in helping you to remember and apply the parameters of simple harmonic motion.

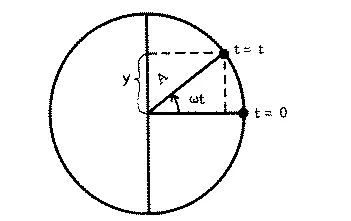
In the above figure, the position of a particle with angular speed  about a circle of radius A is projected onto the vertical diameter. We arbitrarily let the projection be at the center of the diameter at t = 0, and call y the displacement of the projection from the center. Then, at some later time t, the particle will have turned through an angle , equal to t, and the projection will have moved a distance

y = A sin t.

Taking the expression for y and differentiating twice with respect to time, we obtain:

dy/dt = A cos t;

d²y/dt= -² A sin t.

By definition, d²y/dt² is acceleration and ² is a positive constant. From Newton's second law:

F = m d²y/dt²,

F = -m² A sin t.

Therefore, since A sin t = y is the displacement of the projection from the center of the circle, our final equation is

F = -m² y = -ky,

and the projection moves with simple harmonic motion, with the center of the diameter as the equilibrium position.

The circle of radius A is called the reference circle for the harmonic oscillation of amplitude A.

In the figure above, the period of the motion is the time required for one complete vibration. In this time, then, the projection must move from the center of the diameter, up to a maximum positive displacement, down to a maximum negative displacement, and back to the central point.

In the same time, then, the particle moving with angular speed  in a circular path will go just once around the circle. The angle turned through by this particle is 2 rad, and we see, from the definition of angular velocity:

= /t, that = 2/T,

where T is the period of the simple harmonic motion. Also, since the frequency f = 1/T,

= 2f.

Thus, in our equation x = A sin t, the coefficient of t is 2f or 2/T.

Problem:

1. A particle is oscillating harmonically about the origin along the y-axis with amplitude A = 4.0 cm and period T = 2.0 s.
   1. What is the angular speed of the corresponding uniform circular motion?
   2. What is the minimum time required for the particle to travel from

y₁ = -1 cm to y₂ = +2 cm?