Angular Momentum
Why does Earth keep on spinning? What started it spinning to begin with? Why doesn’t Earth’s gravitational attraction not bring the Moon crashing in toward Earth? And how does an ice skater manage to spin faster and faster simply by pulling her arms in? Why does she not have to exert a torque to spin faster?
The answer to these questions is that just as the total linear motion (momentum) in the universe is conserved, so is the total rotational motion conserved. We call the total rotational motion angular momentum, the rotational counterpart to linear momentum. In this chapter, we first define and then explore angular momentum from a variety of viewpoints. First, however, we investigate the angular momentum of a single particle. This allows us to develop angular momentum for a system of particles and for a rigid body.
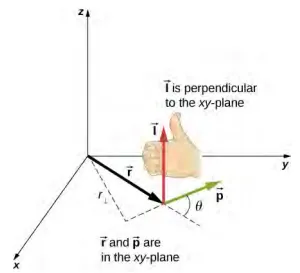
Figure 11.2.111.2.1 shows a particle at a position r⃗ r→ with linear momentum p⃗ p→ = mv⃗ v→ with respect to the origin. Even if the particle is not rotating about the origin, we can still define an angular momentum in terms of the position vector and the linear momentum.
ANGULAR MOMENTUM OF A PARTICLE
The angular momentum l⃗ l→ of a particle is defined as the cross-product of r⃗ r→ and p⃗ p→, and is perpendicular to the plane containing r⃗ r→ and p⃗ p→:
l⃗ =r⃗ ×p⃗ .(11.2.1)(11.2.1)l→=r→×p→.

Figure 11.2.111.2.1: In three-dimensional space, the position vector r⃗ r→ locates a particle in the xy-plane with linear momentum p⃗ p→. The angular momentum with respect to the origin is l⃗ =r⃗ ×p⃗ l→=r→×p→, which is in the z-direction. The direction of l⃗ l→ is given by the right-hand rule, as shown.
The intent of choosing the direction of the angular momentum to be perpendicular to the plane containing r⃗ r→ and p⃗ p→ is similar to choosing the direction of torque to be perpendicular to the plane of r⃗ r→ and F⃗ F→, as discussed in Fixed-Axis Rotation. The magnitude of the angular momentum is found from the definition of the cross-product,
l=rpsinθ,(11.2.2)(11.2.2)l=rpsinθ,
where θθ is the angle between r⃗ r→ and p⃗ p→. The units of angular momentum are kg • m2/s. As with the definition of torque, we can define a lever arm r⊥⊥ that is the perpendicular distance from the momentum vector p⃗ p→ to the origin, r⊥⊥ = r sin θθ. With this definition, the magnitude of the angular momentum becomes
l=r⊥p=r⊥mv.(11.2.3)(11.2.3)l=r⊥p=r⊥mv.
We see that if the direction of p⃗ p→ is such that it passes through the origin, then θθ = 0, and the angular momentum is zero because the lever arm is zero. In this respect, the magnitude of the angular momentum depends on the choice of origin. If we take the time derivative of the angular momentum, we arrive at an expression for the torque on the particle:
dl⃗ dt=dr⃗ dt×p⃗ +r⃗ ×dp⃗ dt=v⃗ ×mv⃗ +r⃗ ×dp⃗ dt=r⃗ ×dp⃗ dt.(11.2.4)(11.2.4)dl→dt=dr→dt×p→+r→×dp→dt=v→×mv→+r→×dp→dt=r→×dp→dt.
Here we have used the definition of p⃗ p→ and the fact that a vector crossed into itself is zero. From Newton’s second law dp⃗ dt=∑F⃗ dp→dt=∑F→, the net force acting on the particle, and the definition of the net torque, we can write
dl⃗ dt=∑τ⃗ .(11.2.5)(11.2.5)dl→dt=∑τ→.
Note the similarity with the linear result of Newton’s second law, dp⃗ dt=∑F⃗ dp→dt=∑F→. The following problem-solving strategy can serve as a guideline for calculating the angular momentum of a particle.