Centrifugal & Centripetal Forces

Centrifugal force is ubiquitous in our daily lives. We experience it when we round a corner in a car or when an airplane banks into a turn. We see it in the spin cycle of a washing machine or when children ride on a merry-go-round. One day it may even provide artificial gravity for space ships and space stations. 

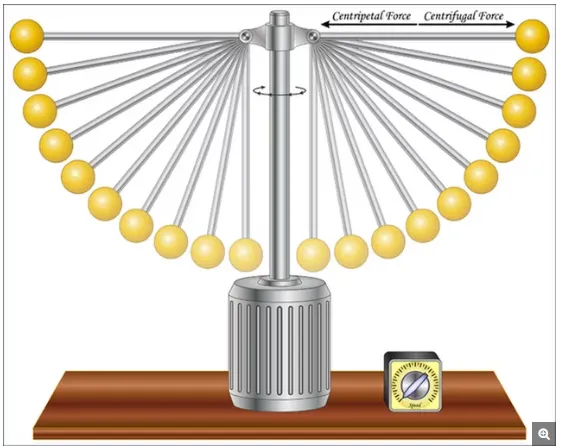
Some people confuse centrifugal force with its counterpart, centripetal force, because they are so closely related. One might say they are two sides of the same coin. Centripetal force is defined as, “The component of force acting on a body in curvilinear motion that is directed toward the center of curvature or axis of rotation,” while centrifugal force is defined as, “The apparent force, equal and opposite to the centripetal force, drawing a rotating body away from the center of rotation, caused by the inertia of the body,” according to the American Heritage Dictionary. 

Note that while centripetal force is an actual force, centrifugal force is defined as an apparent force. In other words, when twirling a mass on a string, the string exerts an inward centripetal force on the mass, while mass appears to exert an outward force on the string. 

“The difference between centripetal and centrifugal force has to do with different ‘frames of reference,’ that is, different viewpoints from which you measure something,” according to Andrew A. Ganse, a research physicist at the University of Washington. If you are observing a rotating system from the outside, you see an inward centripetal force acting to constrain the rotating body to a circular path. However, if you are part of the rotating system, you experience an apparent centrifugal force pushing you away from the center of the circle, even though what you are actually feeling is the inward centripetal force that is keeping you from literally going off on a tangent. 

This apparent outward force is described by Newton’s Laws of Motion. Newton’s First Law states that “A body at rest will remain at rest, and a body in motion will remain in motion unless it is acted upon by an external force.” If a massive body is moving through space in a straight line, its inertia will cause it to continue in a straight line unless an outside force causes it to speed up, slow down or change direction. In order for it to follow a circular path without changing speed, a continuous centripetal force must be continuously applied at a right angle to its path. The radius r of this circle is equal to the mass m times the square of the velocity v divided by the centripetal force F, or r = mv²/F. The force can be calculated by simply rearranging the equation, F= mv²/r. 

There are many applications that exploit centripetal force. One is to simulate the acceleration of a space launch for astronaut training. When a rocket is first launched, it is so laden with fuel and oxidizer that it can barely move. However, as it ascends, it burns fuel at a tremendous rate, continuously losing mass. Newton’s Second Law states that force equals mass times acceleration, or F = ma. 

In most situations, mass remains constant. With a rocket, though, its mass changes drastically, while the force, in this case the thrust of the rocket motors, remains nearly constant. This causes the acceleration toward the end of the boost phase to increase to several times that of normal gravity. NASA uses large centrifuges to test astronauts and prepare them for this extreme acceleration. In this application, the centripetal force is provided by the seat back pushing inward on the astronaut. 

Another application for centripetal force is the laboratory centrifuge, which is used to accelerate the precipitation of particles suspended in liquid. One common use of this technology is for fractionating blood samples. According to Rice University's Experimental Biosciences website, “The unique structure of blood makes it very easy to separate red blood cells from plasma and the other formed elements by differential centrifugation.” Under the normal force of gravity, thermal motion causes continuous mixing which prevents blood cells from settling out of a whole blood sample. However, a typical centrifuge can achieve accelerations that are 600 to 2,000 times that of normal gravity. This forces the heavy red blood cells to settle at the bottom and stratifies the other various components into layers according to their density. 

High-speed gas centrifuges can also be used to separate the lighter and rarer uranium-235 isotope from the heavier and much more common uranium-238. A uranium oxide powder called yellow cake (U₃O₈) is first converted to uranium hexafluoride gas (UF₆) and piped into a spinning cylinder. The heavier U-238 is forced to the outside while the lighter U-235 moves to the inside, where the cylinder is tapped and the gas is piped to the next centrifuge in the array for further enrichment. It takes multiple steps to enrich the gas to just 3 to 5 percent U-235, which is required to fuel nuclear power plants, and many more steps are required to produce highly enriched weapons-grade uranium which is over 90 percent pure U-235. 

According to the Georgia State University website HyperPhysics, this apparent centrifugal force depends on the mass of the object being rotated, times its square of its angular velocity, i.e., its rate of rotation, divided by its distance from the center of rotation. This is expressed as F = mv²/r. This gives rise to an interesting phenomenon. When a container filled with a liquid is rotated at a constant rate, the liquid moves toward the outside of the container against the force of gravity which is pulling down on the liquid trying to flatten it out. The angular velocity increases linearly the farther you get from the center. However, because the effective outward force depends on the square of the angular velocity, the height of the liquid is proportional to the square of the distance from the center. For this reason, the surface takes on the shape of a paraboloid, which happens to be the ideal shape for a telescope mirror. The focal length of the mirror is determined by the rotational rate and can be calculated as f = g/ω², where f is the focal length, g is the acceleration of gravity and ω is the rate of rotation in radians per second (2π radians equals one complete circle).

This is the principle behind a liquid mirror telescope (LMT). LMTs use a reflecting liquid metal (usually mercury) that is rotated so as to form a parabolic reflecting surface. In order to save weight and cost, the bowl containing the mercury is close to the desired parabolic shape so only a thin layer of the liquid metal is needed. The advantage of this system is that it avoids the cost of casting, grinding, polishing, and coating a solid mirror. The disadvantage is that large LMTs can only look straight up and scan the sky as the earth turns. Conversely, smaller LMTs with mirror diameters of a few inches can use flat mirrors in the optical path to look in any direction. 

According to Ganse, “Centripetal force and centrifugal force are really the exact same force, just in opposite directions because they're experienced from different frames of reference.” This brings us to Newton’s Third Law, which states, “For every action, there is an equal and opposite reaction.” Just as gravity causes you to exert a force on the ground, the ground appears to exert an equal and opposite force on your feet. When you are in an accelerating car, the seat exerts a forward force on you just as you appear to exert a backward force on the seat. In the case of a rotating system, the centripetal force pulls the mass inward to follow a curved path, while the mass appears to push outward due to its inertia. In each of these cases, though, there is only one real force being applied, while the other is only an apparent force.