Motion in a Plane

The physical quantities like work, temperature and distance can be represented in day to day life wholly by their magnitude alone. However, the relation of these physical quantities can be explained by the laws of arithmetic. In order to represent physical quantities like acceleration, displacement, and force, the direction is equally essential along with the magnitude. Let us now study Plane Motion. 

Introduction

Velocity refers to a physical vector quantity which is described by both magnitude and direction. The magnitude or scalar absolute value of velocity is referred to as speed. As stated by the Pythagorean Theorem, the magnitude of the velocity vector is given by –

| v | = v =  √ ( v_x ²+ v_y ² )

Acceleration is defined by the rate of change of velocity of an object with respect to time. Numerically or in terms of components, it can be presented as –

a_x =   ddt   v_x

a_y =    ddt   v_y

Motion in a Plane

Motion in a plane is also referred to as a motion in two dimensions. For example, circular motion, projectile motion, etc. For the analysis of such type of motion, the reference point will be made of an origin and the two coordinate axes X and Y.

Motion in a plane refers to the point where we consider motion in two dimensions as only two dimensions makes a plane. Here, considering the above, we take two axes into consideration – generally X-axis or Y – axes. In an attempt to derive the equation of the motion in a plane, we must know about motion in one direction.

Equations of Plane Motion

The equations of motion in a straight line are:

v = u+at

s = ut+1/2 at²

v₂ = u² + 2as

Where,

·         v = final velocity of the particle

·         u = initial velocity of the particle

·         s = displacement of the particle

·         a = acceleration of the particle

·         t = the time interval in which the particle is in consideration

In a plane, we have to apply the same equations separately in both the directions: Y axis and Y-axis. This would give us the equations for motion in a plane.

v_y   = u_y + a_yt

s_y = u_y t +1/2 a_y t²

v²_y   = u²y+2a_y s

Where,

·         v_y = final velocity of the particle in the y-direction

·         u_y = initial velocity of the particle in the y-direction

·         s_y = displacement of the particle in the y-direction

·         a_y = acceleration of the particle in the y-direction

Similarly, for the X-axis :

v_x = u_x + a_x t

s_x=  u_x t+1/2 a_xt²

_v²x = u²_x+2 a_xs

Where,

·         v_x = final velocity of the particle in the x-direction

·         u_x = initial velocity of the particle in the x-direction

·         s_x= displacement of the particle in the x-direction

·         a_x = acceleration of the particle in x-direction

Projectile Motion: Plane Motion

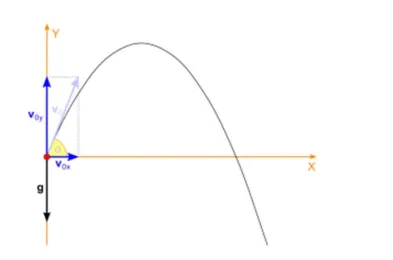
One of the most common examples of motion in a plane is Projectile motion. In a projectile motion, the only acceleration acting is in the vertical direction which is acceleration due to gravity (g). Therefore, equations of motion can be applied separately in the X-axis and Y-axis to find the unknown parameters.

The above diagram represents the motion of an object under the influence of gravity. It is an example of projectile motion (an special case of motion in a plane).

Examples of Two-Dimensional Plane Motion

·          Throwing a ball or a cannonball

·          The motion of a billiard ball on the billiard table.

·          A motion of a shell fired from a gun.

·          A motion of a boat in a river.

·          The motion of the earth around the sun.