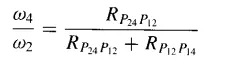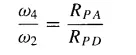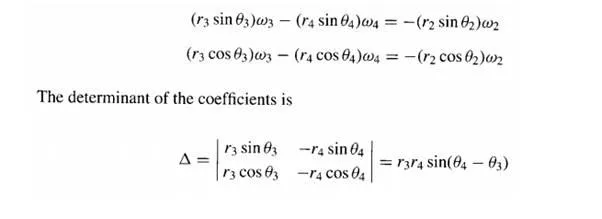
Freudensteins Theorem

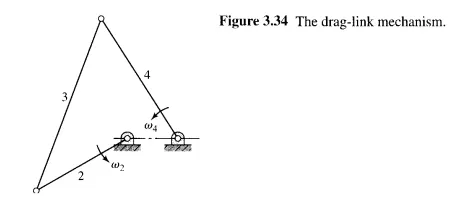
In the analysis and design of linkages it is often important to know the phases of the linkage at which the extreme values of the output velocity occur or, more precisely, the phases at which the ratio of the output and input velocities reaches its extremes. The earliest work in determining extreme values is apparently that of Krause,2 who stated that the velocity ratio W4/W2 of the drag-link mechanism (Fig. 3.34) reaches an extreme value when the connecting rod and follower, links 3 and 4, become perpendicular to each other. Rosenauer, however, showed that this is not strictly true.3 Following Krause, Freudenstein developed a simple graphical method for determining the phases of the four-bar linkage at which the extreme values of the velocity do occur

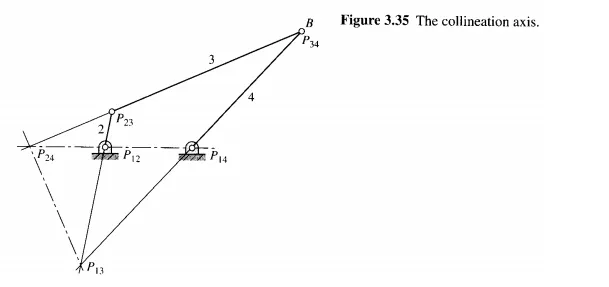
Freudenstein's theorem makes use of the line connecting instant centers P13 and P24 (Fig. 3.35), called the collineation axis. The theorem states that at an extreme of the output to input angular velocity ratio of a four-bar linkage, the collineation axis is perpendicular to the coupler link.

Using the angular-velocity-ratio theorem, Eq. (3.28), we write

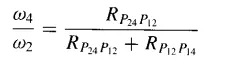
Because R P12 P,4 is the fixed length of the frame link, the extremes of the velocity ratio occur when RP24P12 is either a maximum or a minimum. Such positions may occur on either or both sides of P12.Thus the problem reduces to finding the geometry of the linkage for which RP24P12 is an extremum.

During motion of the linkage, P24 travels along the line P12P14 as seen by the theorem of three centers; but at an extreme value of the velocity ratio, P24 must instantaneously be at rest (its direction of travel on this line must be reversing). This occurs when the velocity of P24, considered as a point of link 3, is directed along the coupler link. This will be true only when the coupler link is perpendicular to the collineation axis, because PI3 is the instant center of link 3.

An inversion of the theorem (treating link 2 as fixed) states that an extreme value of the velocity ratio (J)3/ (J)2 of a four-bar linkage occurs when the collineation axis is perpendicular to the follower (link 4).

Indices of merit; Mechanical advantage

In this section we will study some of the various ratios, angles, and other parameters of mechanisms that tell us whether a mechanism is a good one or a poor one. Many such parameters have been defined by various authors over the years, and there is no common agreement on a single "index of merit" for all mechanisms. Yet the many used have a number of features in common, including the fact that most can be related to the velocity ratios of the mechanism and, therefore, can be determined solely from the geometry of the mechanism. In addition, most depend on some knowledge of the application of the mechanism, especially of which are the input and output links. It is often desirable in the analysis or synthesis of mechanisms to plot these indices of merit for a revolution of the input crank and to notice in particular their minimum and maximum values when evaluating the design of the mechanism or its suitability for a given application.

The ratio of the angular velocity of the output link to the input link of a mechanism is inversely proportional to the segments into which the common instant center cuts the line of centers. Thus, in the four-bar linkage of Fig. 3.36, if links 2 and 4 are the input and output links, respectively, then

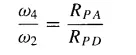
is the equation for the output- to input-velocity ratio. We also learned in Section 3.19 that the extremes of this ratio occur when the collineation axis is perpendicular to the coupler, link 3.

If we now assume that the linkage of Fig. 3.36 has no friction or inertia forces during its operation or that these are negligible compared with the input torque Tz, applied to link 2, and the output torque T4, the resisting load torque on link 4, then we can derive a relation between Tz and T4. Because friction and inertia forces are negligible, the input power applied to link 2 is the negative of the power applied to link 4 by the load; hence

The mechanical advantage of a mechanism is the instantaneous ratio of the output force (torque) to the input force (torque). Here we see that the mechanical advantage is the negative reciprocal of the velocity ratio. Either can be used as an index of merit in judging a mechanism's ability to transmit force or power.

The mechanism is redrawn in Fig. 3.37 at the position where links 2 and 3 are on the same straight line. At this position, Rp A and W4 are passing through zero; hence an extreme