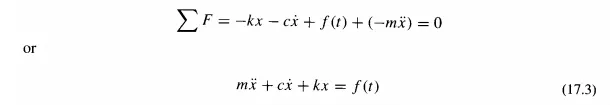
Vibration Analysis

Differential Equations Of Motion

Any motion that exactly repeats itself after a certain interval of time is a periodic motion and is called a vibration. Vibrations may be either free or forced. A mechanical element is said to have a free vibration if the periodic motion continues after the cause of the original disturbance is removed, but if a vibratory motion persists because of the continuing existence of a disturbing force, then it is called a forced vibration. Any free vibration of a mechanical system will eventually cease because of loss of energy. In vibration analysis we often take account of these energy losses by using a single factor called the damping factor. Thus, a heavily damped system is one in which the vibration decays rapidly. The period of a vibration is the time for a single event or cycle; the frequency is the number of cycles or periods occurring in unit time. The natural frequency is the frequency of a free vibration. If the forcing frequency becomes equal to the natural frequency of a system, then resonance is said to occur.

We shall also use the terms steady-state vibration. to indicate that a motion is repeating itself exactly in each successive cycle, and transient vibration, to indicate a vibratory-type motion that is changing in character. If a periodic force operates on a mechanical system, the resulting motion will be transient in character when the force first begins to act, but after an interval of time the transient will decay, owing to damping, and the resulting motion is termed a steady-state vibration.

The word response is frequently used in discussing vibratory systems. The words response, behaviour, and performance have roughly the same meaning when used in dynamic analysis. Thus we can apply an external force having a sine-wave relationship with time to a vibrating system in order to determine how the system "responds," or "behaves," when the frequency of the force is varied. A plot using the vibration amplitude along one axis and the forcing frequency along the other axis is then described as a performance or response curve for the system. Sometimes it is useful to apply arbitrary input disturbances or forces to a system.

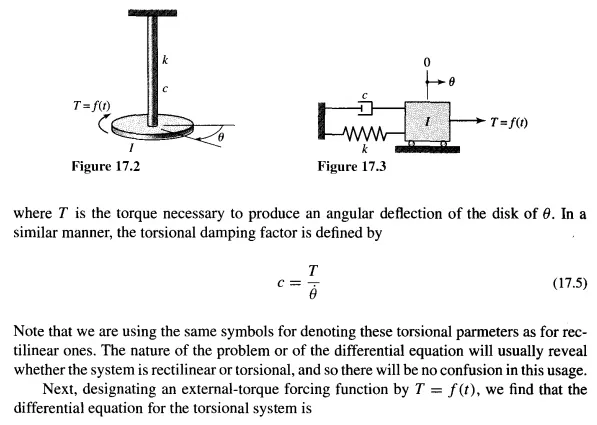
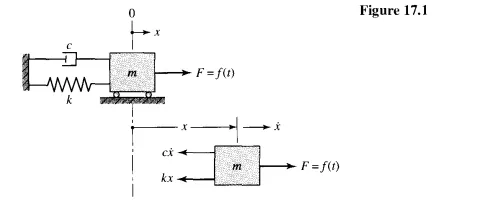
These may not resemble the force characteristics that a real system would receive in use at all; yet the response of the system to these arbitrary disturbances can provide much useful information about the system. Vibration analysis is sometimes called elastic-body analysis or deformable-body analysis, because, as we shall see, a mechanical system must have elasticity in order to allow vibration. When a rotating shaft has a torsional vibration, this means that a mark on the circumference at one end of the shaft is successively ahead of and then behind a corresponding mark on the other end of the shaft. In order words, torsional vibration of a shaft is the alternate twisting and untwisting of the rotating material and requires elasticity for its existence. We shall begin our study of vibration by assuming that elastic parts have no mass and that heavy parts are absolutely rigid-that is, they have no elasticity. Of course these assumptions are never true, and so, in the course of our studies, we must also learn to correct for the effects of making these assumptions.

Figure 17.1 shows an idealized vibrating system having a mass m guided to move only in the x direction. The mass is connected to a fixed frame through the spring k and the dash pot c. The assumptions used are as follows:

1. The spring and the dashpot are massless.

2. The mass is absolutely rigid.

3. All the damping is concentrated in the dashpot.

It turns out that a great many mechanical systems can be analysed quite accurately using these assumptions