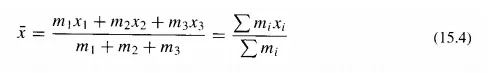
Dynamic Force Analysis {Planar}

Centroid And Center Of Mass

Newton's laws set forth the relationships between the net unbalanced force on a particle, its mass, and its acceleration. For that chapter, because we were only studying systems in equilibrium, we made use of the relationship for entire rigid bodies, arguing that they are made up of collections of particles and that the action and the reaction forces between the particles cancel each other. In this chapter we must be more careful: We must remember that each of these particles may have acceleration, and that the

accelerations of these particles may all be different from each other. Which of these many point accelerations are we to use? And why?

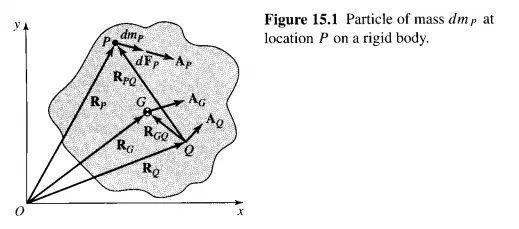
Referring to Fig. 15.1, we consider a particle with a mass dmp at some arbitrary point P on the rigid body shown. For this single particle, Eq. (14.1) tells us that the net unbalanced force dF p on that particle is proportional to its mass and its absolute acceleration Ap:

Our task now is to sum these effects-that is, to integrate over all particles of the body and to put the result in some usable form for rigid bodies other than single particles. As we did in the previous chapter, we can conclude that the action and the reaction forces between particles of the body balance each other, and therefore cancel in the process of the summation. The only net remaining forces are the constraint forces, those whose reactions are on some other body than this one. Thus, integrating Eq. (a) over all particles of mass in our rigid body (number j), we obtain

This important equation is the integrated form of Newton's law for a particle, now extended to a rigid body. Notice that it is the same equation as was given in Eq. (14.1). However, careful derivation of the acceleration term was not done there because we were treating static problems where accelerations were to be set to zero.

We have now answered the question raised earlier in this section. Recognizing that each particle of a rigid body may have a different acceleration, which one should be used? Equation (15.3) shows clearly that the absolute acceleration of the center of mass of the body is the proper acceleration to be used in Newton's law. That particular point, and no other, is the proper point for which Newton's law for a rigid body has the same form as for a single particle.

In solving engineering problems, we frequently find that forces are distributed in some manner over a line, over an area, or over a volume. The resultant of these distributed forces is usually not too difficult to find. In order to have the same effect, this resultant must act at the centroid of the system. Thus, the centroid of a system is a point at which a system of distributed forces may be considered concentrated with exactly the same effect.

Instead of a system of forces, we may have a distributed mass, as in the above derivation. Then, by center of mass we mean the point at which the mass may be considered concentrated so that the effect is the same.

In Fig. 15.2a, a series of particles with masses are shown located at various positions along a line. The center of mass G is located at