Matrix Velocity and Acceleration Analyses

This matrix of coefficients, called the Jacobian, is essential for the solution of any set of derivatives of the joint variables. As was pointed out in Section 3.16, if this matrix becomes singular, there is no unique solution for the velocities (or accelerations) of the joint variables. If this occurs, such a position of the mechanism is called a singular position; one example would be a dead-center position.

The derivatives of the velocity matrices of Eq. (12.27) give rise to definition of a set of acceleration operator matrices

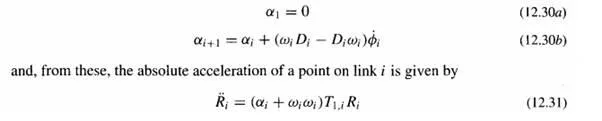
Much further detail and more power has been developed using this transformation matrix approach to the kinematic and dynamic analysis of rigid-body systems