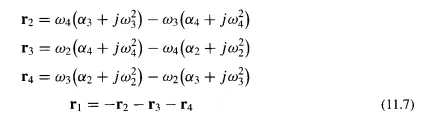
Cognate Linkages; The Roberts-Chebychev Theorem

One of the unusual properties of the planar four-bar linkage is that there is not one but three four-bar linkages that generate the same coupler curve. This was discovered by Roberts9 in 1875 and by Chebychev in 1878 and hence is known as the Roberts-Chebychev theorem. Though mentioned in an English publication in 1954,10 it did not appear in the American literature until it was presented, independently and almost simultaneously, by Richard S. Hartenberg and Jacques Denavit of North-western University and by Roland T. Hinkle of Michigan State University in 1958."

In Fig. 11.22 let OIABOz be the original four-bar linkage with a coupler point P attached to A B. The remaining two linkages defined by the Roberts-Chebychev theorem were termed cognate linkages by Hartenberg and Denavit. Each of the cognate linkages is shown in Fig. 11.22, one using short dashes for showing the links and the other using long dashes. The construction is evident by observing that there are four similar triangles, each containing the angles a, {3,and y, and three different parallelograms.

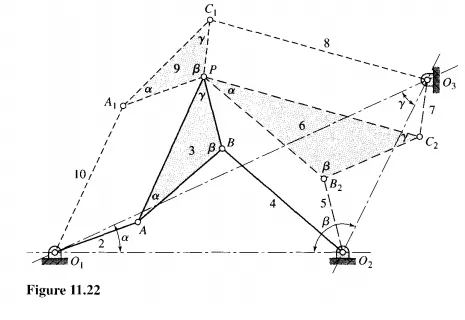
A good way to obtain the dimensions of the two cognate linkages is to imagine that the frame connections OJ, 02, and 03 can be unfastened. Then "pull" 0\, O2, and 03 away from each other until a straight line is formed by the crank, coupler, and follower of each linkage. If we were to do this for Fig. 11.22, then we would obtain Fig. 11.23. Note that the frame distances are incorrect, but all the movable links are of the correct length and all the angles are correct. Given any four-bar linkage and its coupler point, one can create a drawing similar to Fig. 11.23 and obtain the dimensions of the other two cognate linkages. This approach was discovered by A. Cayley and is called the Cayley diagram.

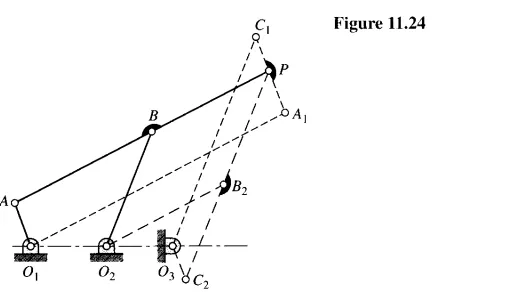
If the tracing point P is on the straight-line AB or its extensions, a figure like Fig. 11.23 is of little help because all three linkages are compressed into a single straight line. An example is shown in Fig. 11.24 where 0\ A B O2 is the original linkage having a coupler point P on an extension of A B. To find the cognate linkages, locate 0\ on an extension of 0\ 02 in the same ratio as AB is to BP. Then construct, in order, the parallelograms O,A, P A, 02B2P B, and 03C, PC2.

Hartenberg and Denavit showed that the angular-velocity relations between the links in Fig. 11.22 are

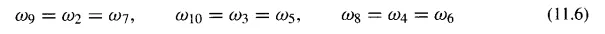
They also observed that if crank 2 is driven at a constant angular velocity and if the velocity relationships are to be preserved during generation of the coupler curve, the cognate mechanisms must be driven at variable angular velocities.

Bloch's Method Of Synthesis

Sometimes a research paper is published that is a classic in its simplicity and cleverness. Such a paper written by the Russian kinematician Bloch has sparked an entire generation of research. We present the method here more for the additional ideas the method may generate than for its intrinsic value, and also for its historic interest.

In Fig. 11.25 replace the links of a four-bar linkage by position vectors and write the vector equation

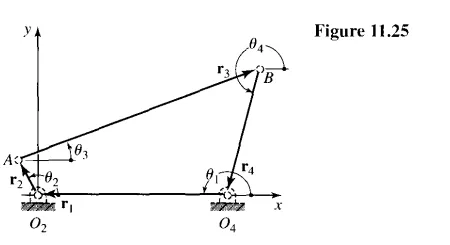
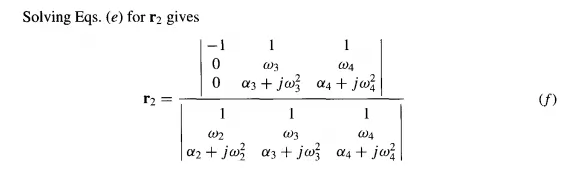
Similar expressions can be obtained for r3 and r4. It turns out that the denominators for all three expressions-that is, for r2, r3, and r4-are complex numbers and are equal. In division, we divide the magnitudes and subtract the angles. Because these denominators are all alike, the effect of the division would be to change the magnitudes of r2, r3, and r4 by the same factor and to shift all the directions by the same angle. For this reason, we make all the denominators unity; the solutions then give dimensionless vectors for the links. When the determinants are evaluated, we find