Three-Position Synthesis

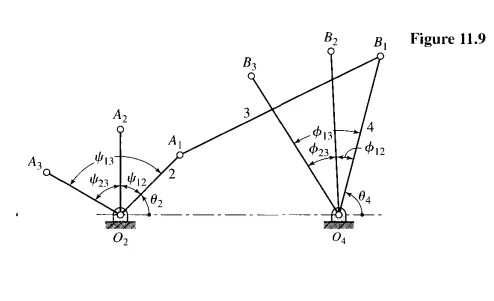
Four-Position Synthesis ; point-Position Reduction

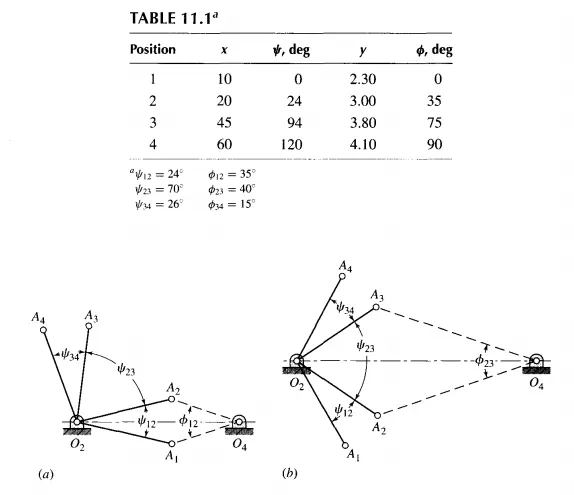
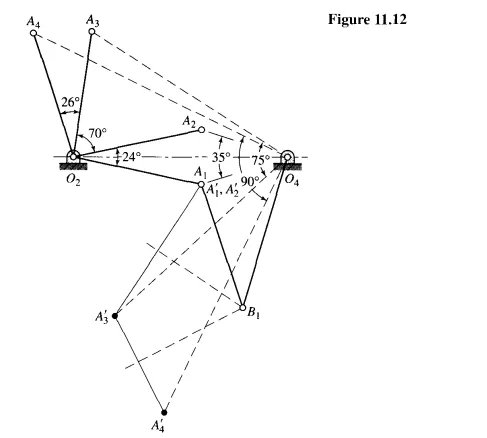
Precision Positions ; Structural Error; Chebychev Spacing

Next we inscribe a regular polygon having 2n sides in this circle, with its first side spaced symmetrically about the x axis. Perpendiculars dropped from each jth vertex now intersect the diameter Llx at the precision position value of Xj. Figure I 1.13b illustrates the construction for the numerical example before.

It should be noted that Chebychev spacing is a good approximation of precision positions that will reduce structural error in the design; depending on the accuracy requirements of the problem, it may be satisfactory. If additional accuracy is required, then by plotting a curve of structural error versus x we can usually determine visually the adjustments to be made in the choice of precision positions for another trial.

Before closing this section, however, we should note two more problems that can arise to confound the designer in using precision positions for synthesis. These are called branch defect and order defect. Branch defect refers to a possible completed design that meets all of the prescribed requirements at each of the precision positions, but which cannot· be moved continuously between these positions without being taken apart and reassembled. Order defect refers to a developed linkage that can reach all of the precision positions, but not in the desired order.