Synthesis of Linkages

Type, Number, And Dimensional Synthesis

Type synthesis refers to the kind of mechanism selected; it might be a linkage, a geared system, belts and pulleys, or even a earn system. This beginning phase of the total design problem usually involves design factors such as manufacturing processes, materials, safety, space, and economics. The study of kinematics is usually only slightly involved in type synthesis.

Number synthesis deals with the number of links and the number of joints or pairs that are required to obtain a certain mobility. Number synthesis is the second step in design following type synthesis.

The third step in design, determining the dimensions of the individual links, is called dimensional synthesis. This is the subject of the balance of this chapter

Function Generation, Path Generation, And Body Guidance

A frequent requirement in design is that of causing an output member to rotate, oscillate, or reciprocate according to a specified function of time or function of the input motion. This is called function generation. A simple example is that of synthesizing a four-bar linkage to generate the function y = f(x). In this case, x would represent the motion (crank angle) of the input crank, and the linkage would be designed so that the motion (angle) of the output rocker would approximate the function y. Other examples of function generation are as follows:

1. In a conveyor line the output member of a mechanism must move at the constant. velocity of the conveyor while performing some operation-for example, bottle capping, return, pick up the next cap, and repeat the operation.

2. The output member must pause or stop during its motion cycle to provide time for another event. The second event might be a sealing, stapling, or fastening operation of some kind.

3. The output member must rotate at a specified nonuniform velocity function because it is geared to another mechanism that requires such a rotating motion.

A second type of synthesis problem is called path generation. This refers to a problem in which a coupler point is to generate a path having a prescribed shape. Common requirements are that a portion of the path be a circular arc, elliptical, or a straight line. Sometimes it is required that the path cross over itself, as in a figure-of-eight.

The third general class of synthesis problems is called body guidance. Here we are interested in moving an object from one position to another. The problem may call for a simple translation or a combination of translation and rotation. In the construction industry, for example, heavy parts such as scoops and bulldozer blades must be moved through a series of prescribed positions.

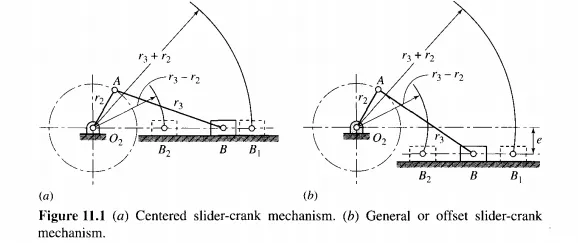
Two-Position Synthesis Of Slider-Crank Mechanisms

The centered slider-crank mechanism of Fig. 11.1a has a stroke B] B2 equal to twice the crank radius r2. As shown, the extreme positions of Bl and B2, also called limiting positions of the slider, are found by constructing circular arcs through O2 of length r3 - r2 and r3 + r2, respectively.

In general, the centered slider-crank mechanism must have r3 larger than r2. However, the special case of r) = r2 results in the isosceles slider-crank mechanism, in which the slider reciprocates through 02 and the stroke is four times the crank radius. All points on the coupler of the isosceles slider crank generate elliptic paths. The paths generated by points on the coupler of the slider crank of Fig. ll.la are not elliptical, but they are always symmetrical about the sliding axis O2 B.

The linkage of Fig. 11.1b is called the general or offset slider-crank mechanism. Certain special effects can be obtained by changing the offset distance e. For example, the