Mobility

One of the first concerns in either the design or the analysis of a mechanism is the number of degrees of freedom, also called the mobility of the device. The mobility* of a mechanism is the number of input parameters (usually pair variables) that must be controlled independently in order to bring the device into a particular position. Ignoring for the moment certain exceptions to be mentioned later, it is possible to determine the mobility of a mechanism directly from a count of the number of links and the number and types of joints that it includes.

To develop this relationship, consider that before they are connected together, each link of a planar mechanism has three degrees of freedom when moving relative to the fixed link. Not counting the fixed link, therefore, an n-link planar mechanism has 3(n - I) degrees of freedom before any of the joints are connected. Connecting a joint that has one degree of freedom, such as a revolute pair, has the effect of providing two constraints between the connected links. If a two-degree-of-freedom pair is connected, it provides one.

*The German literature distinguishes between movability and mobility. Movability includes the six degrees of freedom of the device as a whole, as though the ground link were not fixed, and thus applies to a kinematic chain. Mobility neglects these and considers only the internal relative motions, thus applying to a mechanism. The English literature seldom recognizes this distinction, and the terms are used somewhat interchangeably

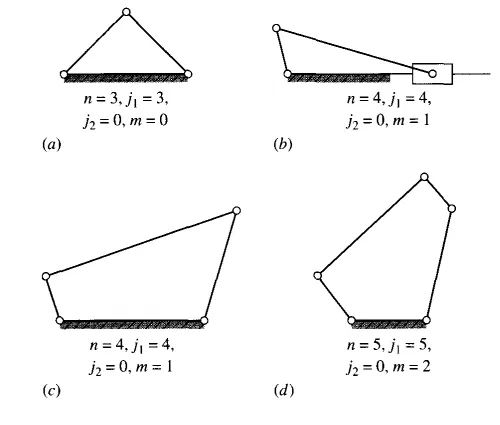
Figure 1.3 Application of the kutzbach mobility criterion

constraint. When the constraints for all joints are subtracted from the total freedoms of the unconnected links, we find the resulting mobility of the connected mechanism. When we use h to denote to number of single-degree-of- freedom pairs and h for the number of two degree-of-freedom pairs, the resulting mobility m of a planar n-link mechanism is given by

Written in this form, Eq. (1.1) is called the Kutzbach criterion for the mobility of a planar mechanism. Its application is shown for several simple cases in Fig. 1.3.

If the Kutzbach criterion yields m > 0, the mechanism has m degrees of freedom. If m = 1, the mechanism can be driven by a single input motion. If m = 2, then two separate input motions are necessary to produce constrained motion for the mechanism; such a case is shown in Fig. 1.3d. If the Kutzbach criterion yields m = 0, as in Fig. 1.3a, motion is impossible, and the mechanism forms a structure. If the criterion gives m = -lor less, then there are redundant constraints in the chain and it forms a statically indeterminate structure. Examples are shown in Fig. 1.4. Note in these examples that when three links are joined by a single pin, two joints must be counted; such a connection is treated as two separate but concentric pairs.

Figure 1.5 shows examples of Kutzbach's criterion applied to mechanisms with two degree-of-freedom joints. Particular attention should be paid to the contact (pair) between the wheel and the fixed link in Fig. 1.5b. Here it is assumed that slipping is possible

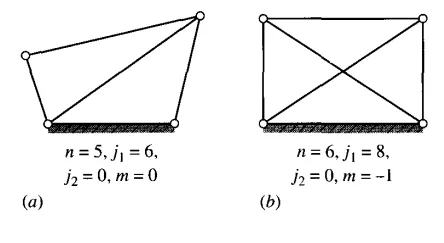
Figure 1.4 Applications of the kutzbach criterion to structures

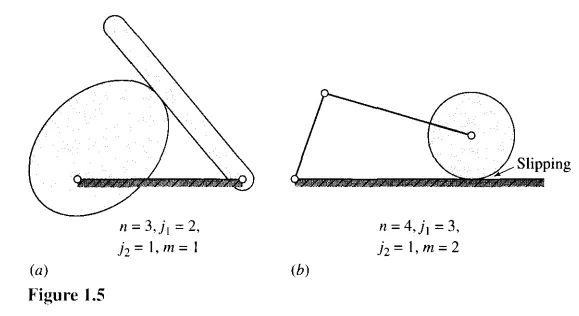
between the links. If this contact included gear teeth or if friction was high enough to prevent slipping, the joint would be counted as a one-degree-of-freedom pair, because only one relative motion would be possible between the links.

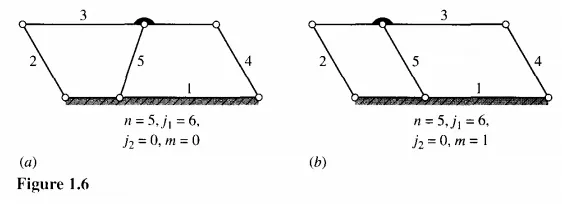
Sometimes the Kutzbach criterion gives an incorrect result. Notice that Fig. 1.6a represents a structure and that the criterion properly predicts m = O. However, if link 5 is arranged as in Fig. 1.6b, the result is a double-parallelogram linkage with a mobility of 1 even though Eq. (1.1) indicates that it is a structure. The actual mobility of 1 results only if the parallelogram geometry is achieved. Because in the development of the Kutzbach criterion no consideration was given to the lengths of the links or other dimensional properties, it is not surprising that exceptions to the criterion are found for particular cases with equal link lengths, parallel links, or other special geometric features.

Even though the criterion has exceptions, it remains useful because it is so easily applied. To avoid exceptions, it would be necessary to include all the dimensional properties of the mechanism. The resulting criterion would be very complex and would be useless at the early stages of design when dimensions may not be known.

An earlier mobility criterion named after Griibler applies to mechanisms with only single-degree-of-freedom joints where the overall mobility of the mechanism is unity. Putting h = 0 and m = I into Eq. (1.1), we find Griibler's criterion for planar mechanisms with constrained motion:

From this we can see, for example, that a planar mechanism with a mobility of 1 and only single-degree-of-freedom joints cannot have an odd number of links. Also, we can find the simplest possible mechanism of this type; by assuming all binary links, we find

n = jl = 4. This shows why the four-bar linkage (Fig. 1.3c) and the slider-crank mechanism (Fig. 1.3b) are so common in application.

Both the Kutzbach criterion, Eq. (1.1), and the Griibler criterion, Eq. (1.2), were derived for the case of planar mechanisms. If similar criteria are developed for spatial mechanisms, we must recall that each unconnected link has six degrees of freedom; and each revolute pair, for example, provides five constraints. Similar arguments then le<\dto the three-dimensional form of the Kutzbach criterion,

The simplest form of a spatial mechanism,* with all single-freedom pairs and a mobility of 1, is therefore n = j I = 7