Static CMOS Logic

The principle of static CMOS logic is shown in Fig. A.13(a): the output is connected to ground through an n-block and to  through a dual p-block (the gate in Fig. A.8 is also an example). Without changes of the inputs this gate consumes only the leakage currents of some transistors. When it is switching it draws an additional current which is needed to charge and discharge the internal capacitances. and the load. Although the gate's logic function is ideally independent of the transistor channel widths, they determine the dynamic behavior essentially: wider transistors will switch a capacitive load faster, but they will also cause a larger input capacitance of the gate. Unless otherwise noted, minimum-width and, of course, minimum-channel-length transistors are assumed. For given capacitances the transistors' on-state current  will limit the switching speed of the gate and, consequently, the maximum clock frequency of a synchronous circuit (cf. Section A.3)

Two other important parameters determining the speed are the so-called f

an-in  which is the number of inputs of a gate, and the fan-out  which is the number of unity loads (i.e., inputs) connected to a gate's output. For a static-CMOS NAND gate as shown in Fig. A.14 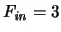 means that three transistors are connected in series, which is roughly equivalent to one longer transistor which can conduct only 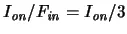. The effect of  is an -fold load capacitance. This could lead to the assumption that the gate delay is is proportional to both  and . However, the situation is more complex and (see Section 3.1.5). Another fact to be considered is that a large fan-in will degrade the normalized noise margins if the transistor sizes W are not adapted accordingly.

One way to improve speed is to make the output less sensitive to the capacitive load by inserting a buffer as shown in Fig. A.13(b). Note that the input  must be inverted and the logic blocks must be replaced by their duals in order to perform the same logic function 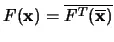.