Applications of Differentiation

Linear Approximation

A linear approximation is an approximation of a general function using a linear function.

In mathematics, a linear approximation is an approximation of a general function using a linear function (more precisely, an affine function). Linear approximations are widely used to solve (or approximate solutions to) equations. Linear approximation is achieved by using Taylor’s theorem to approximate the value of a function at a point.

Given a twice continuously differentiable function f of one real variable, Taylor’s theorem states that:

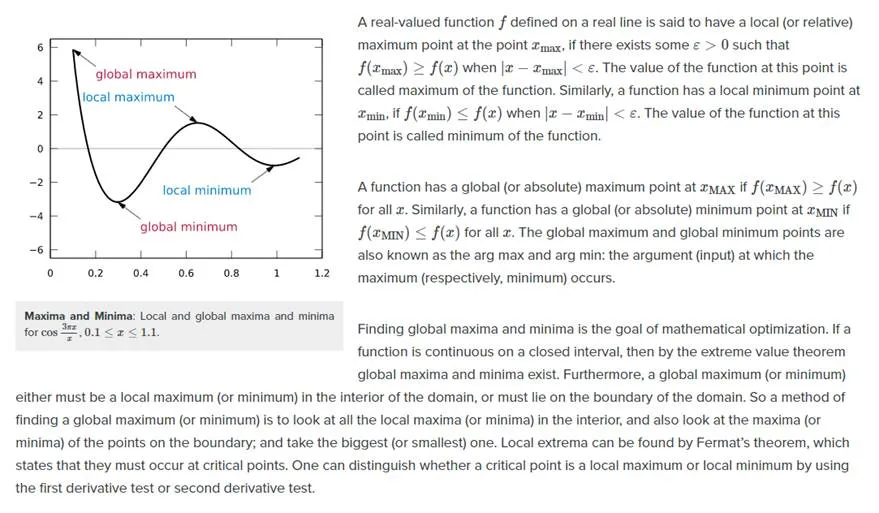
In mathematics, the maximum and minimum (plural: maxima and minima) of a function, known collectively as extrema (singular: extremum), are the largest and smallest value that the function takes at a point either within a given neighborhood (local or relative extremum) or on the function domain in its entirety (global or absolute extremum).

The Mean Value Theorem, Rolle’s Theorem, and Monotonicity

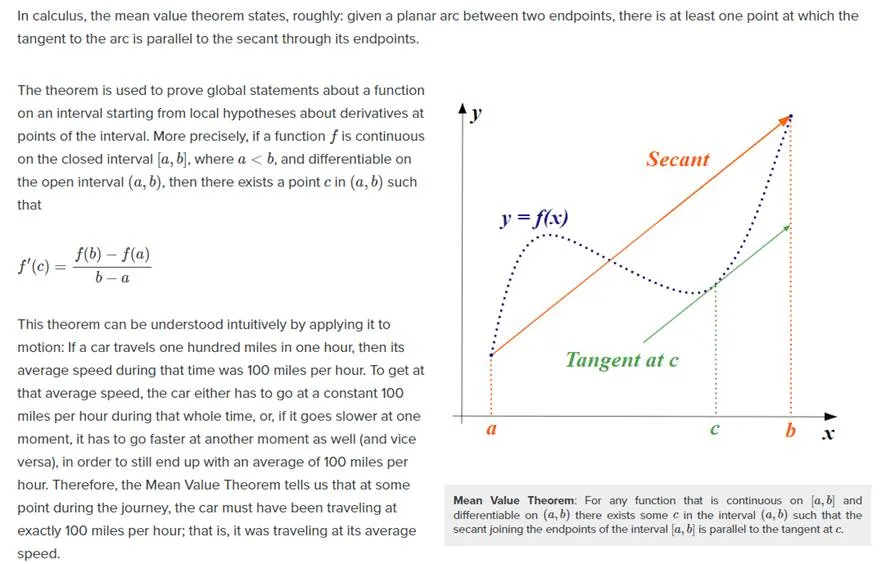
The MVT states that for a function continuous on an interval, the mean value of the function on the interval is a value of the function.

Derivatives and the Shape of the Graph

The shape of a graph may be found by taking derivatives to tell you the slope and concavity.

Derivative: At each point, the derivative of is the slope of a line that is tangent to the curve. The line is always tangent to the blue curve; its slope is the derivative. Note derivative is positive where a green line appears, negative where a red line appears, and zero where a black line appears.