Nyquist Sampling Theorem

In the sampling process, while converting the analog signal to a discrete version, the chosen sampling signal is the most important factor. And what are the reasons to get distortions in the sampling output while conversion of analog to discrete? These types of questions can be answered by the “Nyquist sampling theorem”.

Nyquist sampling theorem states that the sampling signal frequency should be double the input signal’s highest frequency component to get distortion less output signal. As per the scientist’s name, Harry Nyquist this is named as Nyquist sampling theorem.

Fs=2Fm

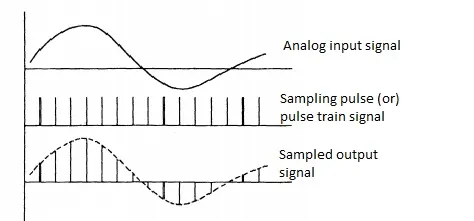
Sampling Output Waveforms

The sampling process requires two input signals. The first input signal is an analog signal and another input is sampling pulse or equidistance pulse train signal. And the output which is then sampled signal comes from the multiplier block. The sampling process output waveforms are shown below.

Sampling-output-waveforms

Shannon Sampling Theorem

The sampling theorem is one of the efficient techniques in the communication concepts for converting the analog signal into discrete and digital form. Later the advances in digital computers Claude Shannon, an American mathematician implemented this sampling concept in digital communications for converting the analog to digital form. The sampling theorem is a very important concept in communications and this technique should follow the Nyquist criteria for avoiding the aliasing effect.

Applications

There are few applications of sampling theorem are listed below. They are

·         To maintain sound quality in music recordings.

·         Sampling process applicable in the conversion of analog to discrete form.

·         Speech recognition systems and pattern recognition systems.

·         Modulation and demodulation systems

·         In sensor data evaluation systems

·         Radar and radio navigation system sampling is applicable.

·         Digital watermarking and biometric identification systems, surveillance systems.