What is the Sampling Theorem?

A signal has three properties like voltage or amplitude, frequency, phase. The signals are represented only in an analog form where the digital form of technology is not available. Analog signals are continuous in time and difference in voltage levels for different periods of the signal. Here, the main drawback of this is, the amplitude keeps on changing along with the period of the signal. This can be overcome by the digital form of signal representation. Here conversion of an analog form of the signal into digital form can be done using the sampling technique. The output of this technique represents the discrete version of its analog signal. Here in this article, you can find what is sampling theorem, definition, applications, and its types.

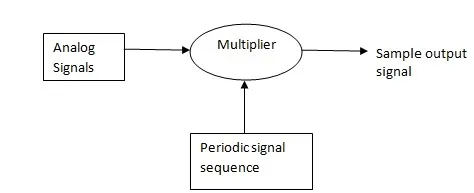
A continuous signal or an analog signal can be represented in the digital version in the form of samples. Here, these samples are also called as discrete points. In sampling theorem, the input signal is in an analog form of signal and the second input signal is a sampling signal, which is a pulse train signal and each pulse is equidistance with a period of “Ts”. This sampling signal frequency should be more than twice of the input analog signal frequency. If this condition satisfies, analog signal perfectly represented in discrete form else analog signal may be losing its amplitude values for certain time intervals. How many times the sampling frequency is more than the input analog signal frequency, in the same way, the sampled signal is going to be a perfect discrete form of signal. And these types of discrete signals are well performed in the reconstruction process for recovering the original signal.

sampling-block-diagram

sampling Theorem Definition

The sampling theorem can be defined as the conversion of an analog signal into a discrete form by taking the sampling frequency as twice the input analog signal frequency. Input signal frequency denoted by Fm and sampling signal frequency denoted by Fs.

The output sample signal is represented by the samples. These samples are maintained with a gap, these gaps are termed as sample period or sampling interval (Ts). And the reciprocal of the sampling period is known as “sampling frequency” or “sampling rate”. The number of samples is represented in the sampled signal is indicated by the sampling rate

Sampling frequency Fs=1/Ts

Sampling Theorem Statement

Sampling theorem states that “continues form of a time-variant signal can be represented in the discrete form of a signal with help of samples and the sampled (discrete) signal can be recovered to original form when the sampling signal frequency Fs having the greater frequency value than or equal to the input signal frequency Fm.

If the sampling frequency (Fs) equals twice the input signal frequency (Fm), then such a condition is called the Nyquist Criteria for sampling. When sampling frequency equals twice the input signal frequency is known as “Nyquist rate”.

Fs=2Fm

If the sampling frequency (Fs) is less than twice the input signal frequency, such criteria called an Aliasing effect.

Fs<2Fm

So, there are three conditions that are possible from the sampling frequency criteria. They are sampling, Nyquist and aliasing states. Now we will see the Nyquist sampling theorem.