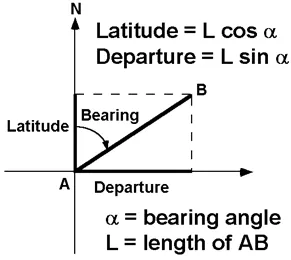
LATITUDES AND DEPARTURES

The latitude of a line is its projection on the north-south meridian and is equal to the length of the line times the cosine of its bearing.

• The departure of a line is its projection on the east-west meridian and is equal to the length of the line times the sine of its bearing.
• The latitude is the y component of the line (also known as northing), and the departure is the x component of the line (also known as easting).

 CLOSURE OF LATITUDES AND DEPARTURES

• The algebraic sum of all latitudes must equal zero or the difference in latitude between the initial and final control points
• The algebraic sum of all departures must equal zero or the difference in departure between the initial and final control points
• If the sums of latitudes and departures do not equal zero, corrections must be made.

 DEGREE and RADIAN MEASURE

Trigonometric functions require input data to be stored in radian measure, but the field measurements are in degrees. Therefore a conversion is necessary. Remember that there are 2*pi radians in a circle.

• To convert from degrees to radians, multiply by azimuth by pi/180
• To convert from radians to degrees, multiply by radians by 180/pi

 CALCULATION OF LATITUDES AND DEPARTURES (Using azimuths)

For example, look at the calculation of latitude for the angle from station A to station B:

With a calculator:

26° 10' = 26.16667°

26.16667° * pi/180 = 0.4566945 rad

cos(0.4566945 rad) = 0.897515

0.897515 + 285.10 ft = 255.88 ft

Or in one operation using R:

cos((26 + 10/60) * pi/180) * 285.1
[1] 255.8815

likewise for departure

sin((26 + 10/60) * pi/180) * 285.1
[1] 125.7245

or in Excel:

SIN((26 + 10/60) * PI()/180) * 285.1 = 125.7245

As you can see, setting this up in Excel is fairly straightforward. You will have a record of your measurements and any transformations of those measurements, and it will allow you to check your work easily.

 ADJUSTMENT OF LATITUDES AND DEPARTURES

In order to calculate corrections for latitude and departure there is a simple formula called the Compass (or Bowditch) Rule, which is used when angles and distances are measured with the same relative accuracy. There are other methods for different measurement accuracy differentials as well, but this method is simple to implement and works well enough for our purposes.

For example, look at line AB.

correction in latitude = -total latitude misclosure / traverse perimeter * length of AB = -(-0.71 / 2466.05 * 285.1) = 0.08

correction in departure = -total departure misclosure / traverse perimeter * length of AB = -(0.53 / 2466.05 * 285.1) = -0.06

 Once you have calculated the correction factors, simply add these to the original latitudes and departures to get balanced latitude and departure values..

For example, again look at line AB

original latitude AB + correction = 255.85 + 0.08 = 255.96

original departure AB + correction = 125.72 + (-0.06) = 125.66

Also make sure that your balanced latitudes and departures sum to zero, respectively.