Analysis of Space Trusses Using Method of Tension Coefficients

1. Tension Co-efficient Method

The tension co efficient for a member of a frame is defined as the pull or tension in that member is divided by its length.

t = T/l Where t = tension co efficient for the member

T= Pull in the member

l = Length

2. Analysis Procedure Using Tension Co-efficient - 2D Frames

1. List the coordinates of each joint (node)of the truss.

2. Determine the projected lengths Xij and Yij of each member of the truss. Determine the support lengths lij of each member using the equation lij =?Xij2+Yij2

3. Resolve the the applied the forces at the joint in the X and Y directions. Determine the support reactions and their X and Y components.

4. Identify a node with only two unknown member forces and apply the equations of equilibrium. The solution yields the tension co efficient for the members at the node.

5. Select the next joint with only two unknown member forces and apply the equations of equilibrium and apply the tension co efficient.

6. Repeat step 5 till the tension co efficient of all the members are obtained. 7. Compute the member forces from the tension co efficient obtained as above using

Tij= tijx lij

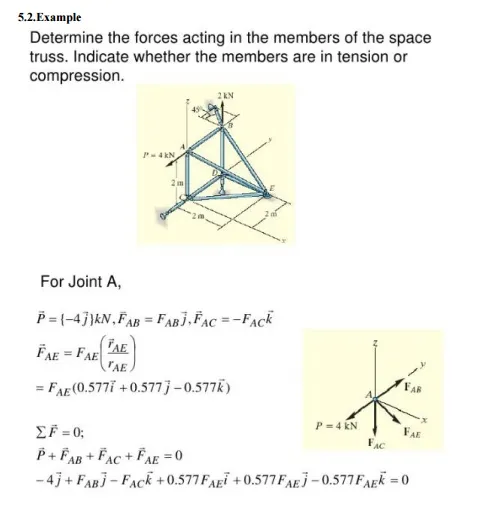
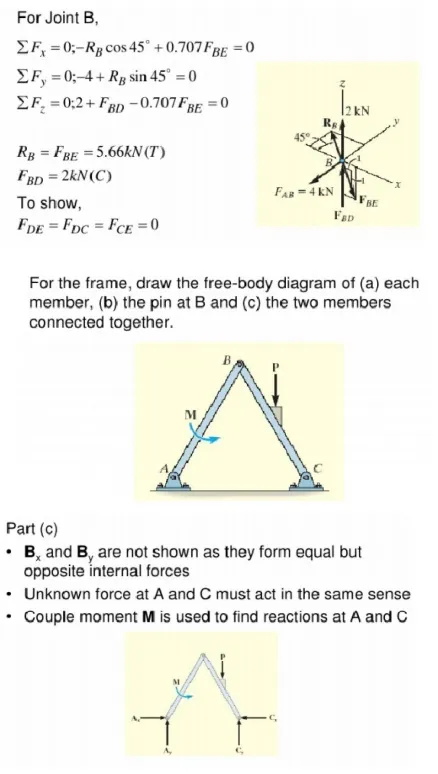
 3. Analysis Procedure Using Tension Co-efficient - Space Frames

1. In step 2 above the projected lengths Zij in the directions are also computed. Determine the support lengths lij of each member using the equation lij =?Xij2+Yij2 +Zij2

2. In step 3 above the components of forces and reactions in the Z directions are also to be determined.

3. In step 4 and 5,each time, nodes with not more than three unknown member forces are to be considered.

Tetrahedron: simplest element of stablespacetruss  ( six members, four joints) expand by adding 3members and1jointeachtime

Determinacy and Stability b+r <3j unstable

b+r=3j statically determinate (check stability)

b+r>3j statically indeterminate (check stability)

Internal Forces

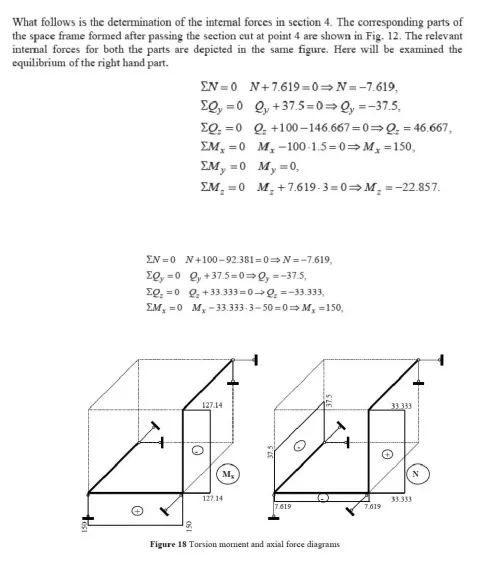
In order to obtain the internal forces at a specified point, we should make section cut perpendicular to the axis of the member at this point. This section cut divides the structure in two parts. The portion of the structure removed from the part in to consideration should be replaced  by the internal forces. The internal forces ensure the equilibrium of the isolated part subjected to the action of external loads and support reactions. A free body diagram of either segment of the  cut member is isolated and the internal loads could be derived by the six equations of equilibrium applied to the segment in to consideration.

Example

In the following example we shall construct the internal forces diagrams for the given in Fig. space frame structure. The introduced global coordinate system is  shown in the same figure.

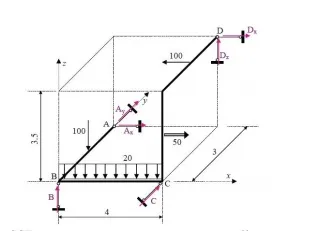
The introduced local coordinate systems of the different elements of the space frame are presented in Fig. The typical  sections where the internal forces must be calculated, in order to construct the relevant diagrams, are numbered from 1 to 8 in the same figure. The typical  sections are placed atleast at the beginning and at the end of each element (segment) of the frame. The internal forces diagrams, in the limits of each element, could be derived by using the corresponding reference and base diagrams.