Stiffness Matrix Method

The given indeterminate structure is first made kinematic ally determinate by introducing constraints atthenodes. The required number of constraints is equal to degrees of freedom at the nodes that is kinematic indeterminacy ?k. The kinematic ally determinate structure comprises of fixed ended members, hence, all nodal displacements are zero. These results in stress resultant discontinuities at these nodes under the action of applied loads or in other words the clamped joints are not in equilibrium.

Inorder to restore the equilibrium of stress resultants at the nodes the nodes are imparted suitable unknown displacements. The number of simultaneous equations represen ting joint equilibrium of forces is equal to kinematic indeterminacy ?k. Solution of these equations gives unknown nodal displacements. Using stiffness properties of members the memberend forces are computed and hence the internal forces through out the structure.

Since nodal displacements are unknowns, the method is also called displacement method. Since  equilibrium conditions are applied at the joints the method is also called equilibrium method. Since stiffness properties of members are used the method is also called stiffness method.

In the displacement method of analysis the equilibrium equations are written by expressing the unknown joint displacements in terms of loads by using load-displacement relations. The unknown joint displacements (the degrees of freedom of the structure) are calculated by solving equilibrium equations. The slope -deflection and moment - distribution methods were extensively used before the high speed computing era. After the revolution in computer industry, only direct stiffness method is used.

PROPERTIES OFTHESTIFFNESS MATRIX

The properties of the stiffness matrix are:

·         It is asymmetric matrix

·         The sum of elements in any column must be equal to zero.

·         It is an unstable element therefore the determinant is equal to zero.

 ELEMENT AND GLOBAL STIFFNESS MATRICES

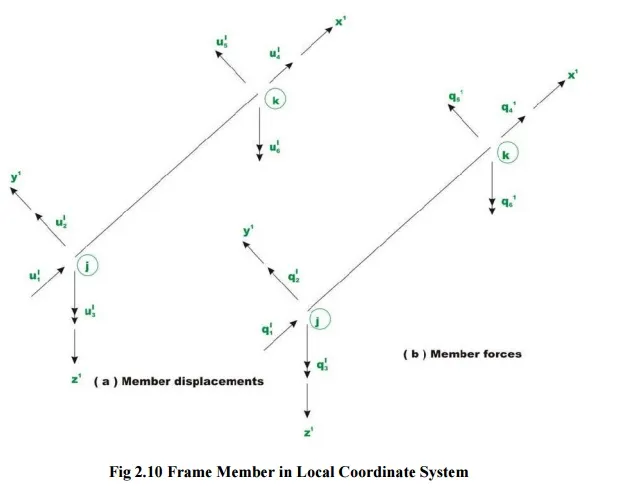
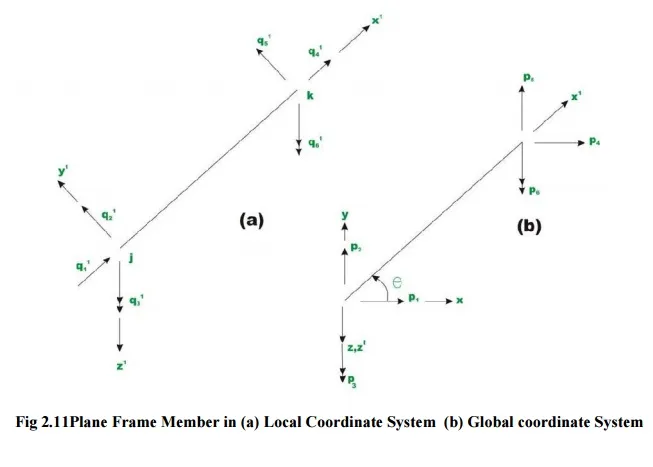
Local co ordinates

In the analysis for convenience we fix the element coordinates coincident with the member axis called element (or) local coordinates (coordinates defined along the individual member axis )

Global co ordinates

It is normally necessary to define a coordinate system dealing with the entire structure is called system on global coordinates (Common coordinate system dealing with the entire structure)

Transformation matrix 

The connectivity matrix which relates the internal forces Q and the external forces R is known as the force transformation matrix. Writing it in a matrix form,

 {Q} =[b]{R}

 Where Q=member force matrix/vector, b=force transformation matrix R = external force/load matrix/ vector

ANALYSIS OF CONTINUOUS BEAMS

ANALYSIS OF PIN JOINTED PLANE FRAMES

An introduction to the stiffness method was given in the previous Page. The basic principles involved in the analysis of beams, trusses were discussed. The problems were solved with hand computation by the direct application of the basic principles. The procedure discussed in the session (page) though      enlighteningarenot suitable for computer programming. It is necessary   to   keesphand computation to a minimum while implementing this procedure on the computer.

In  this session a  formal approach has been  discussed which may  be readily  programmed on  a computer. In this less on the direct stiffness method as applied to planar truss structure is discussed.

Planetrusses are made up of short thin members inter connected a thin gesto form triangulated patterns. Ahinge connection can only transmit forces from one member to another member but not the moment.   For  analysis purpose,  the truss is loaded  at the joints.  Hence,  a truss member is subjected to only axial forces and the forces remain constant along the length of the member. The forces in the member at its two ends must be of the same magnitude but actin the opposite directions for equilibrium as shown in Fig.2.8