Comparisons of Measures of Dispersion

When data are described by a measure of central tendency (mean, median, or mode), all the scores are summarized by a single value. Reports of central tendency are commonly supplemented and complemented by including a measure of dispersion. The measures of dispersion you have just seen differ in ways that will help determine which one is most useful in a particular situation.

Range. Of all the measures of dispersion, the range is the easiest to determine. It is commonly used as a preliminary indicator of dispersion. However, because it takes into account only the scores that lie at the two extremes, it is of limited use.

Quartile Scores are based on more information than the range and, unlike the range, are not affected by outliers. However, they are only infrequently used to describe dispersion because they are not as easy to calculate as the range and they do not have the mathematical properties that make them so useful as standard deviation and variance.

The standard deviation ( or s) and variance ( or s²) are more complete measures of dispersion which take into account every score in a distribution. The other measures of dispersion we have discussed are based on considerably less information. However, because variance relies on the squared differences of scores from the mean, a single outlier has greater impact on the size of the variance than does a single score near the mean. Some statisticians view this property as a shortcoming of variance as a measure of dispersion, especially when there is reason to doubt the reliability of some of the extreme scores. For example, a researcher might believe that a person who reports watching television an average of 24 hours per day may have misunderstood the question. Just one such extreme score might result in an appreciably larger standard deviation, especially if the sample is small. Fortunately, since all scores are used in the calculation of variance, the many non-extreme scores (those closer to the mean) will tend to offset the misleading impact of any extreme scores.

The standard deviation and variance are the most commonly used measures of dispersion in the social sciences because:

• Both take into account the precise difference between each score and the mean. Consequently, these measures are based on a maximum amount of information.
• The standard deviation is the baseline for defining the concept of standardized score or "z-score".
• Variance in a set of scores on some dependent variable is a baseline for measuring the correlation between two or more variables (the degree to which they are related).

Comparing Measures of Dispersion
Look at the distributions for the given variables. Compare the shapes of the distributions, their ranges and outliers, and answer the questions.

How Data Determines the Measures of Dispersion
Here is an activity that allows you to see how individual data points determine the different measures of dispersion. Click and drag to move points around, and notice when and how the measures change.

Standardized Distribution Scores, or "Z-Scores"

Actual scores from a distribution are commonly known as a "raw scores." These are expressed in terms of empirical units like dollars, years, tons, etc. We might say "The Smith family's income is $29,418." To compare a raw score to the mean, we might say something like "The mean household income in the U.S. is $2,232 above the Smith family's income." This difference is an absolute deviation of 2,232 emirical units (dollars, in this example) from the mean.

When we are given an absolute deviation from the mean, expressed in terms of empirical units, it is difficult to tell if the difference is "large" or "small" compared to other members of the data set. In the above example, are there many families that make less money than the Smith family, or only a few? We were not given enough information to decide.

We get more information about deviation from the mean when we use the standard deviation measure presented earlier in this tutorial. Raw scores expressed in empirical units can be converted to "standardized" scores, called z-scores. The z-score is a measure of how many units of standard deviation the raw score is from the mean. Thus, the z-score is a relative measure instead of an absolute measure. This is because every individual in the dataset affects value for the standard deviation. Raw scores are converted to standardized z-scores by the following equations:

where   is the population mean,   is the sample mean,   is the population standard deviation, s is the sample standard deviation, and x is the raw score being converted.

For example, if the mean of a sample of I.Q. scores is 100 and the standard deviation is 15, then an I.Q. of 128 would correspond to:

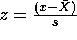 = (128 - 100) / 15 = 1.87

For the same distribution, a score of 90 would correspond to:

z = (90 - 100) / 15 = - 0.67

A positive z-score indicates that the corresponding raw score is above the mean. A negative z-score represents a raw score that is below the mean. A raw score equal to the mean has a z-score of zero (it is zero standard deviations away).

Z-scores allow for control across different units of measure. For example, an income that is 25,000 units above the mean might sound very high for someone accustomed to thinking in terms of U.S. dollars, but if the unit is much smaller (such as Italian Lires or Greek Drachmas), the raw score might be only slightly above average.  Z-scores provide a standardized description of departures from the mean that control for differences in size of empirical units.

When a dataset conforms to a "normal" distribution, each z-score corresponds exactly to known, specific percentile score. If a researcher can assume that a given empirical distribution approximates the normal distribution, then he or she can assume that the data's z-scores approximate the z-scores of the normal distribution as well. In this case, z-scores can map the raw scores to their percentile scores in the data.

As an example, suppose the mean of a set of incomes is $60,200, the standard deviation is $5,500, and the distribution of the data values approximates the normal distribution. Then an income of $69,275 is calculated to have a z-score of 1.65. For a normal distribution, a z-score of 1.65 always corresponds to the 95th percentile. Thus, we can assume that $69,275 is the 95th percentile score in the empirical data, meaning that 95% of the scores lie at or below $69,275.

The normal distribution is a precisly defined, theoretical distribution. Empirical distributions are not likely to conform perfectly to the normal distribution. If the data distribution is unlike the normal distribution, then z-scores do not translate to percentiles in the "normal" way. However, to the extent that an empirical distribution approximates the normal distribution, z-scores do translate to percentiles in a reliable way.