Total Probability Theorem
The probability is the likelihood of an event. The probability of an event going to happen is 1 and for an impossible event is 0. In probability theory, there exists a fundamental rule that relates to the marginal probability and the conditional probability, which is called formula or the law of the total probability. Through several distinct events, it expresses the total probability of an event. Here, we are going to discuss the law of total probability, its statement, proof along with its example.
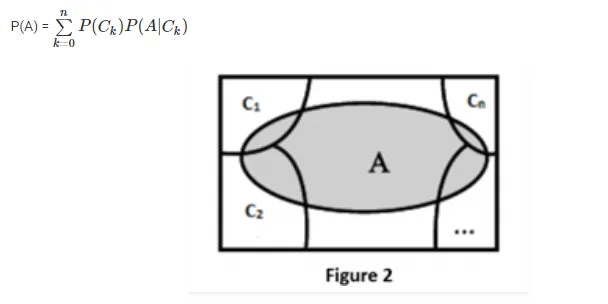
For two events A and B associated with a sample space S, the sample space can be divided into a set A ∩ B′, A ∩ B, A′ ∩ B, A′ ∩ B′. This set is said to be mutually disjoint or pairwise disjoint because any pair of sets in it is disjoint. Elements of this set are better known as a partition of sample space.
This can be represented by the Venn diagram as shown in fig. 1. In cases where the probability of occurrence of one event depends on the occurrence of other events, we use total probability theorem.
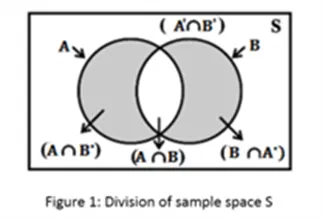
Let events C1, C2 . . . Cn form partitions of the sample space S, where all the events have a non-zero probability of occurrence. For any event, A associated with S, according to the total probability theorem,