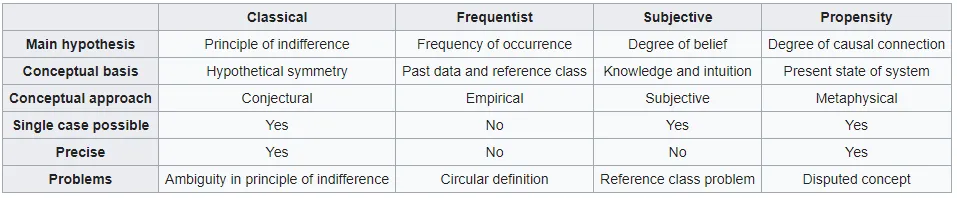
Probability interpretations

The word probability has been used in a variety of ways since it was first applied to the mathematical study of games of chance. Does probability measure the real, physical tendency of something to occur or is it a measure of how strongly one believes it will occur, or does it draw on both these elements? In answering such questions, mathematicians interpret the probability values of probability theory.

There are two broad categories of probability interpretations which can be called "physical" and "evidential" probabilities. Physical probabilities, which are also called objective or frequency probabilities, are associated with random physical systems such as roulette wheels, rolling dice and radioactive atoms. In such systems, a given type of event (such as a die yielding a six) tends to occur at a persistent rate, or "relative frequency", in a long run of trials. Physical probabilities either explain, or are invoked to explain, these stable frequencies. The two main kinds of theory of physical probability are frequentist accounts (such as those of Venn,^[3] Reichenbach^[4] and von Mises^[5]) and propensity accounts (such as those of Popper, Miller, Giere and Fetzer).

Evidential probability, also called Bayesian probability, can be assigned to any statement whatsoever, even when no random process is involved, as a way to represent its subjective plausibility, or the degree to which the statement is supported by the available evidence. On most accounts, evidential probabilities are considered to be degrees of belief, defined in terms of dispositions to gamble at certain odds. The four main evidential interpretations are the classical (e.g. Laplace's) interpretation, the subjective interpretation (de Finetti and Savage), the epistemic or inductive interpretation (Ramsey, Cox) and the logical interpretation (Keynes and Carnap). There are also evidential interpretations of probability covering groups, which are often labelled as 'intersubjective' (proposed by Gillies  and Rowbottom).

Some interpretations of probability are associated with approaches to statistical inference, including theories of estimation and hypothesis testing. The physical interpretation, for example, is taken by followers of "frequentist" statistical methods, such as Ronald Fisher, Jerzy Neyman and Egon Pearson. Statisticians of the opposing Bayesian school typically accept the existence and importance of physical probabilities, but also consider the calculation of evidential probabilities to be both valid and necessary in statistics. This article, however, focuses on the interpretations of probability rather than theories of statistical inference.

The terminology of this topic is rather confusing, in part because probabilities are studied within a variety of academic fields. The word "frequentist" is especially tricky. To philosophers it refers to a particular theory of physical probability, one that has more or less been abandoned. To scientists, on the other hand, "frequentist probability" is just another name for physical (or objective) probability. Those who promote Bayesian inference view "frequentist statistics" as an approach to statistical inference that recognises only physical probabilities. Also the word "objective", as applied to probability, sometimes means exactly what "physical" means here, but is also used of evidential probabilities that are fixed by rational constraints, such as logical and epistemic probabilities.

It is unanimously agreed that statistics depends somehow on probability. But, as to what probability is and how it is connected with statistics, there has seldom been such complete disagreement and breakdown of communication since the Tower of Babel. Doubtless, much of the disagreement is merely terminological and would disappear under sufficiently sharp analysis.

Philosophy

The philosophy of probability presents problems chiefly in matters of epistemology and the uneasy interface between mathematical concepts and ordinary language as it is used by non-mathematicians. Probability theory is an established field of study in mathematics. It has its origins in correspondence discussing the mathematics of games of chance between Blaise Pascal and Pierre de Fermat in the seventeenth century,^[15] and was formalized and rendered axiomatic as a distinct branch of mathematics by Andrey Kolmogorov in the twentieth century. In axiomatic form, mathematical statements about probability theory carry the same sort of epistemological confidence within the philosophy of mathematics as are shared by other mathematical statements.

The mathematical analysis originated in observations of the behaviour of game equipment such as playing cards and dice, which are designed specifically to introduce random and equalized elements; in mathematical terms, they are subjects of indifference. This is not the only way probabilistic statements are used in ordinary human language: when people say that "it will probably rain", they typically do not mean that the outcome of rain versus not-rain is a random factor that the odds currently favor; instead, such statements are perhaps better understood as qualifying their expectation of rain with a degree of confidence. Likewise, when it is written that "the most probable explanation" of the name of Ludlow, Massachusetts "is that it was named after Roger Ludlow", what is meant here is not that Roger Ludlow is favored by a random factor, but rather that this is the most plausible explanation of the evidence, which admits other, less likely explanations.

Thomas Bayes attempted to provide a logic that could handle varying degrees of confidence; as such, Bayesian probability is an attempt to recast the representation of probabilistic statements as an expression of the degree of confidence by which the beliefs they express are held.

Though probability initially had somewhat mundane motivations, its modern influence and use is widespread ranging from evidence-based medicine, through six sigma, all the way to the probabilistically checkable proof and the string theory landscape.

A summary of some interpretations of probability

Classical definition

Main article: Classical definition of probability

The first attempt at mathematical rigour in the field of probability, championed by Pierre-Simon Laplace, is now known as the classical definition. Developed from studies of games of chance (such as rolling dice) it states that probability is shared equally between all the possible outcomes, provided these outcomes can be deemed equally likely.^[1] (3.1)

The theory of chance consists in reducing all the events of the same kind to a certain number of cases equally possible, that is to say, to such as we may be equally undecided about in regard to their existence, and in determining the number of cases favorable to the event whose probability is sought. The ratio of this number to that of all the cases possible is the measure of this probability, which is thus simply a fraction whose numerator is the number of favorable cases and whose denominator is the number of all the cases possible.

The classical definition of probability works well for situations with only a finite number of equally-likely outcomes.

This can be represented mathematically as follows: If a random experiment can result in N mutually exclusive and equally likely outcomes and if N_A of these outcomes result in the occurrence of the event A, the probability of A is defined by

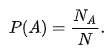
There are two clear limitations to the classical definition.^[18] Firstly, it is applicable only to situations in which there is only a 'finite' number of possible outcomes. But some important random experiments, such as tossing a coin until it rises heads, give rise to an infinite set of outcomes. And secondly, you need to determine in advance that all the possible outcomes are equally likely without relying on the notion of probability to avoid circularity—for instance, by symmetry considerations.

Frequentism

Frequentists posit that the probability of an event is its relative frequency over time, (3.4) i.e., its relative frequency of occurrence after repeating a process a large number of times under similar conditions. This is also known as aleatory probability. The events are assumed to be governed by some random physical phenomena, which are either phenomena that are predictable, in principle, with sufficient information (see determinism); or phenomena which are essentially unpredictable. Examples of the first kind include tossing dice or spinning a roulette wheel; an example of the second kind is radioactive decay. In the case of tossing a fair coin, frequentists say that the probability of getting a heads is 1/2, not because there are two equally likely outcomes but because repeated series of large numbers of trials demonstrate that the empirical frequency converges to the limit 1/2 as the number of trials goes to infinity.

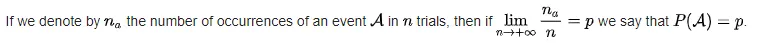
The frequentist view has its own problems. It is of course impossible to actually perform an infinity of repetitions of a random experiment to determine the probability of an event. But if only a finite number of repetitions of the process are performed, different relative frequencies will appear in different series of trials. If these relative frequencies are to define the probability, the probability will be slightly different every time it is measured. But the real probability should be the same every time. If we acknowledge the fact that we only can measure a probability with some error of measurement attached, we still get into problems as the error of measurement can only be expressed as a probability, the very concept we are trying to define. This renders even the frequency definition circular

For frequentists, the probability of the ball landing in any pocket can be determined only by repeated trials in which the observed result converges to the underlying probability in the long run.