Static Indeterminacy of Structures

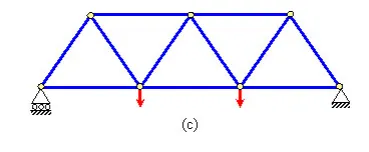
Figure 1.11 Statically determinate structures

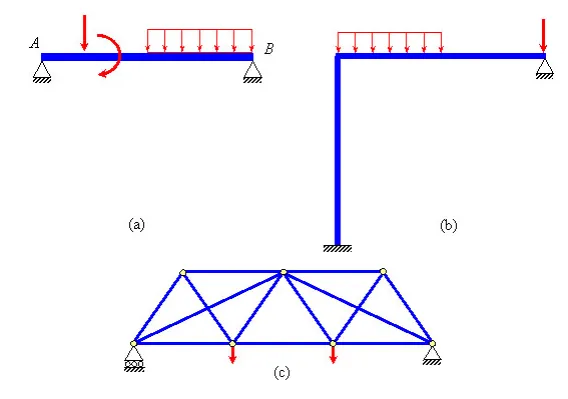
Figure 1.12 Statically indeterminate structures

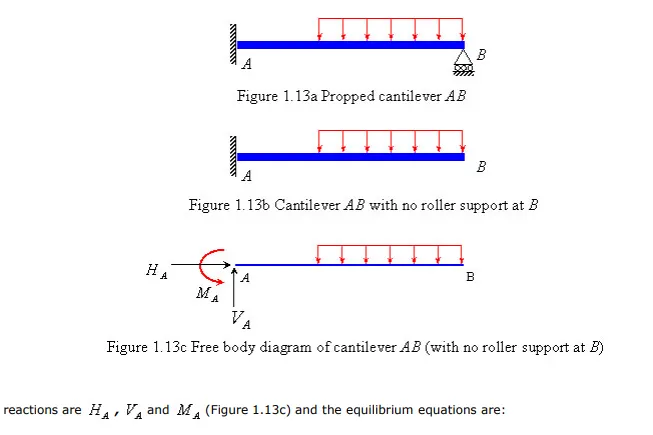
In Section 1.2, the equilibrium equations are described as the necessary and sufficient conditions to maintain the equilibrium of a body. However, these equations are not always able to provide all the information needed to obtain the unknown support reactions and internal forces. The number of external supports and internal members in a system may be more than the number that is required to maintain its equilibrium configuration. Such systems are known as indeterminate systems and one has to use compatibility conditions and constitutive relations in addition to equations of equilibrium to solve for the unknown forces in that system. For an indeterminate system, some support(s) or internal member(s) can be removed without disturbing its equilibrium. These additional supports and members are known as redundants . A determinate system has the exact number of supports and internal members that it needs to maintain the equilibrium and no redundants. If a system has less than required number of supports and internal members to maintain equilibrium, then it is considered unstable . For example, the two-dimensional propped cantilever system in (Figure 1.13a) is an indeterminate system because it possesses one support more than that are necessary to maintain its equilibrium. If we remove the roller support at end B (Figure 1.13b), it still maintains equilibrium. One should note that here it has the same number of unknown support reactions as the number of independent static equilibrium equations. The unknown

v

v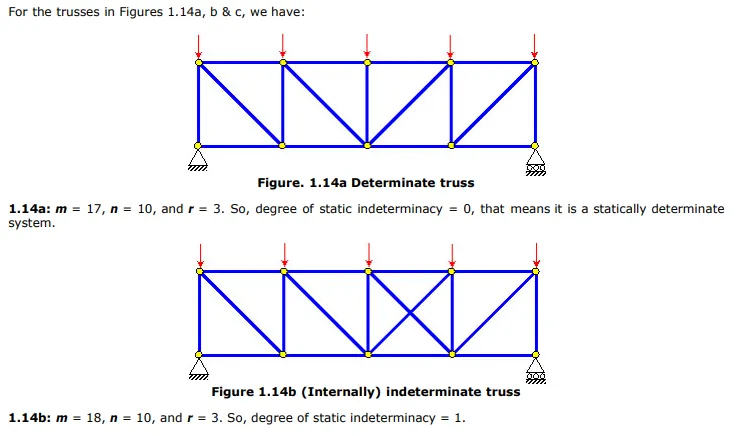

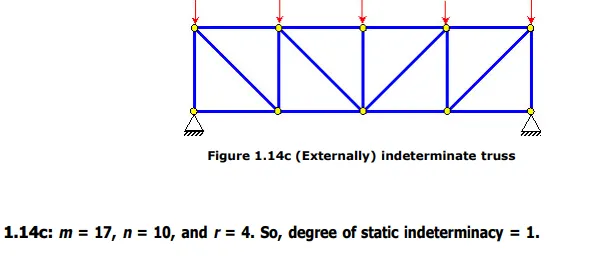
It should be noted that in case of 1.14b, we have one member more than what is needed for a determinate system (i.e., 1.14a), where as 1.14c has one unknown reaction component more than what is needed for a determinate system. Sometimes, these two different types of redundancy are treated differently; as internal indeterminacy and external indeterminacy . Note that a structure can be indeterminate either externally or internally or both externally and internally. We can group external and internal forces (and equations) separately, which will help us understand easily the cases of external and internal indeterminacy. There are r numbers of external unknown forces, which are the support reactions components. We can treat 3 system equilibrium equations as external equations. This will lead us to: Degree of external static indeterminacy = r - 3. The number of internal unknown forces is m and we are left with (2 n -3) equilibrium equations. The 3 system equilibrium equations used earlier were not independent of joint equilibrium equations, so we are left with (2 n - 3) equations instead of 2 n numbers of equations. So: Degree of internal static indeterminacy = m - (2 n - 3)

Please note that the above equations are valid only for two-dimensional pin-jointed truss systems. For example, for three-dimensional ( “space” ) pin-jointed truss systems, the degree of static indeterminacy is given by ( m + r - 3 n ). Similarly, the expression will be different for systems with rigid (fixed) joints, frame members, etc.