What’s Wrong With A Soil Bearing Pressure In Tension?

A young lady structural designer that I was working with was once perplexed with this concept. And what made it more blurred for her was when engineers from the other group doing a portion adjacent to our area also encountered soil bearing in tension to which they tend to dismiss it like it’s no big deal. This got her even more confused and it is about this predicament that she consulted me.

Nope we can’t dismiss it, I told her and explained to her what you will read below in a moment. I wish that she was finally convinced, and I do hope that she was able to put her doubts to rest.

Soil in Tens.. what?!

Ok, on a simplistic representation, it looks something like this:

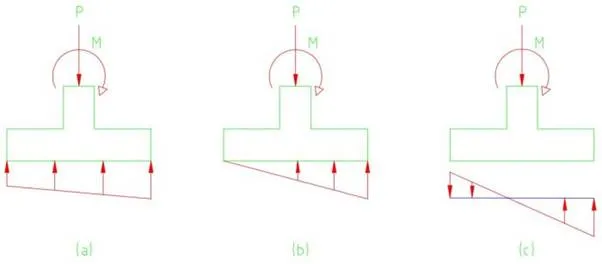
The footing in figure (a) is subjected to gravity loads with a fair amount bending moment (you’ll see what I mean about fair in a while) as evident in the trapezoidal bearing pressure. This is assuming that the pad is infinitely rigid in bending such that the P/A +/- My/I is applicable. The more we increase this bending moment however, one end of the footing will approach a condition where there will be zero bearing pressure as shown in figure (b). Increasing this bending moment further will have a portion of its end flying, that is it will no longer be in contact with soil and hence figure (c) with a tensile soil bearing pressure.

But(!) the bearing pressure in figure (c) is erroneous. Why? Soil can only support loads that are pressed into it and not the ones going away from it. Soil cannot pull back the footing down like a hook is attached at the bottom to prevent it from imminent take off. Unlike piles where the longitudinal reinforcement are embedded into the footing, we cannot assume the soil to take any tensile stresses.

What do I do when I encounter a flying footing?

First, you can either do something about the geometry to totally avoid the tensile bearing pressure or you can live with it and just take measures to account for the loss of bearing area due to the footing losing contact with the soil.

And in addition to our case, the design manager told her that there can’t be no soil tension and to try to run a non-linear analysis.

We tried to iterate options on modifying the geometry but we’re getting rather exaggerated results like the mat foundation is too massive. And in compliance as well to the instructions of the design manager, I told her to run a separate non-linear analysis.

Just to set the correct expectations however, I told her, that running a non-linear analysis cannot and will not eliminate the tensile bearing pressure. It will only prove that a soil bearing in tension phenomenon is indeed present.

What will the computer program do when running a non-linear analysis?

Considering the figures below:

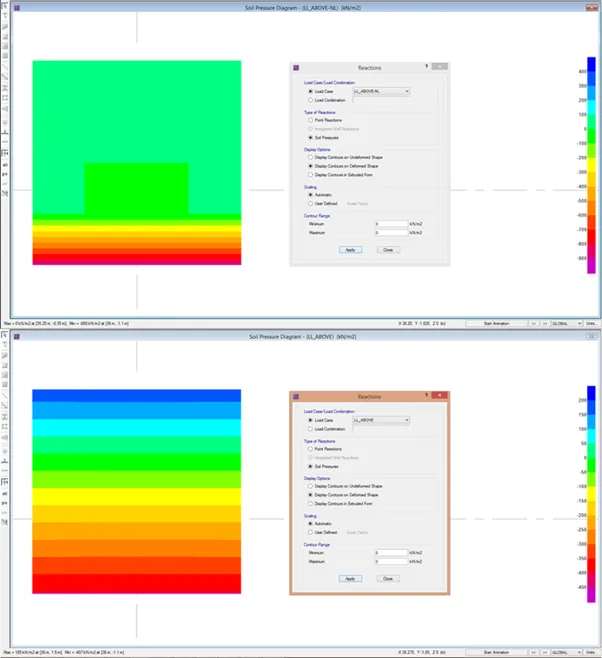Bearing: Linear vs Nonlinear

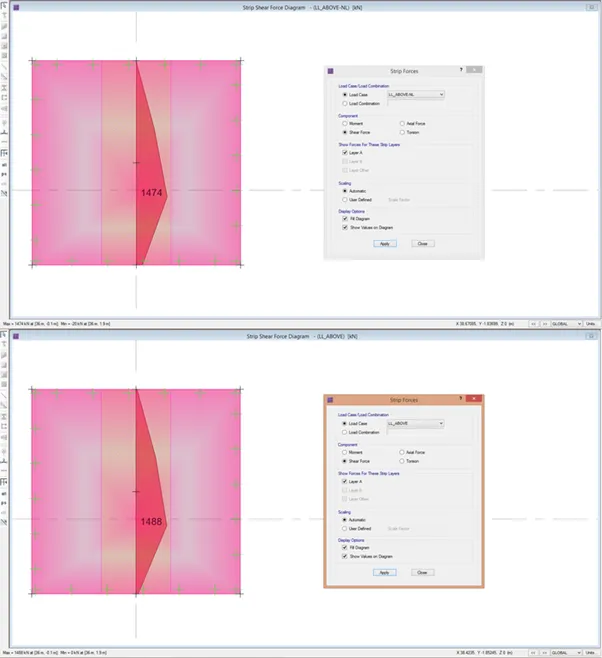Shear: Linear vs Nonlinear

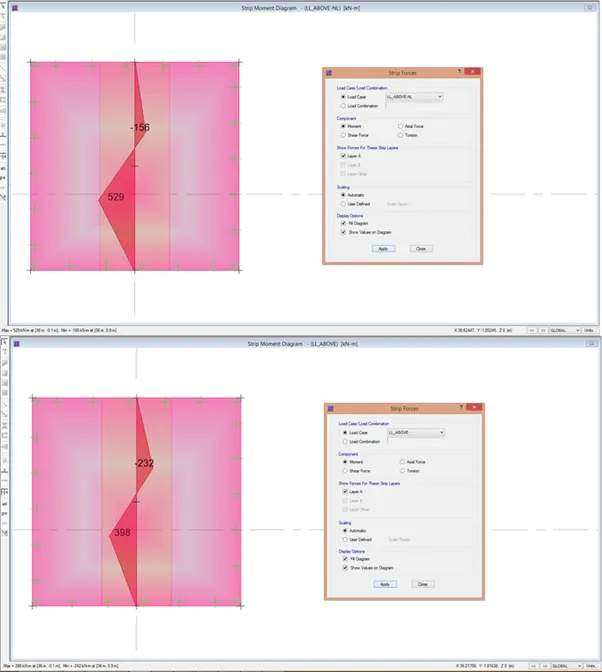Bending Moment: Linear vs Nonlinear

The snapshots showed the differences in bearing pressure and resulting forces using linear and nonlinear run. What nonlinear analysis will do is that it will iterate solutions such that the resulting bearing pressure will have zero bearing pressure on portions of the footing not in contact with the soil. Subsequently, the resulting shears and bending moments will also change, hence, using the forces in the linear load combinations (with uplift) for design will be incorrect and will render erroneous and under-designed footings.

And let’s say that the allowable bearing capacity is only 500 kPa. It can be seen that in the linear run, the bearing pressure is only 407 kPa but in the nonlinear run, the actual bearing reaches almost 890 kPa which is considered failed.

After proving the existence of uplift, what now?

Like I’ve said earlier, you can change the geometry until such time that there is no more soil bearing in tension. In that way you can still use the defined load combinations, which are linear, for design. This is in fact the more viable solution so that you won’t have to worry about the error in load distribution when you have uplift.