How To Check Accidental Torsion In Etabs Using Static Seismic Loads

I hope you would bear with this rather lengthy post.

I have received an email from a reader requesting for a discussion about the correct and proper way of computing the torsional amplification factor Ax for response spectrum cases, how to do it using ETABS’ outputs and how to get the computed value back to ETABS.

It took me quite a while to write this because the topics related to this such as rigid and non-rigid diaphragms keep bouncing in my head. Much effort had been undertaken to gather my thoughts regarding this so here it goes. In the meanwhile, let’s focus first to the torsion induced using static seismic loads.

But before we continue I would like to remind everyone reading my posts that what you read are based on my structural engineering experiences only. If you want a standard procedure or a manual please check out the publications of ASCE and UBC among others, that tackle these issues in far greater depth. And if you find anything related to our discussions in this blog that’s different from what I’ve presented thus far, can I ask you to please share it with me so that I can assess and correct my views accordingly? Thanks in advance.

Now let’s get down to business.

Credit goes to the original owner of this.webp

Ideally, we would not let our building twist too much or at least limit it such that it will be kept to a minimum as much as possible. But as of now, you might have already gotten used to the truth that we don’t have absolute control where we can put our verticals (walls and columns; with the exception of extreme circumstances where lateral stability is ultra-critical) such that we can effectively control this lateral twist. So it will always be dang near impossible for the center of mass and center of rigidity to coincide.

And as such is why codes stipulate minimum requirements to account for this.

How does this torsion affect a building anyway?

V = V/A +/- Tr/J; T = V*e

As you can see, torsional stresses do not just come directly from applied loads (the expression V divided by the area A). More often than not, it’s the twist that’s causing much of the damage. The larger the eccentricity e which magnifies the torsional moment T, the larger the shear stresses are especially in the buildings’ extremities (where r is at maximum).

And just in case you’re still wondering, amplifying this torsion should not change the total base shear that our building is subjected into. However large this eccentricity is, we would always arrive at the equation: summation of forces (either along X or Y) = 0.

By the way, the latest version of ETABS can give us the average and maximum displacements per floor and per diaphragm assignment. But since I am not sure how ETABS exactly arrive at such displacement values, what I’m going to share is the old school way of determining Ax.

Again, the essence of this torsion check is, if at all possible, there should be a minimum twist when a building is subjected to seismic loads in one principal direction. But since this can never be guaranteed, we are hereby obliged to amplify this torsion. It is important to note that codes specify a minimum initial deviation of 5% from the center of mass, in addition to the actual distance between the center of mass and the center of rigidity denoted by e, before we apply Ax such that the resulting final eccentricity is

Total eccentricity = e ± Ax*0.05*L

Where L is the dimension of the structure perpendicular to the direction of the applied force

The maximum allowable value of Ax is 3.0 where it renders 0.15 when multiplied by the initial eccentricity of 5% (for UBC97 refer to 1630.7; and for ASCE7-10, refer to 12.8.4.3).

Having said all that, the load combinations that must be used should be the following. Note that for each seismic load case, a minimum of 5% eccentricity should be specified. P for EXP and EYP denotes positive eccentricity and N denotes a negative eccentricity.

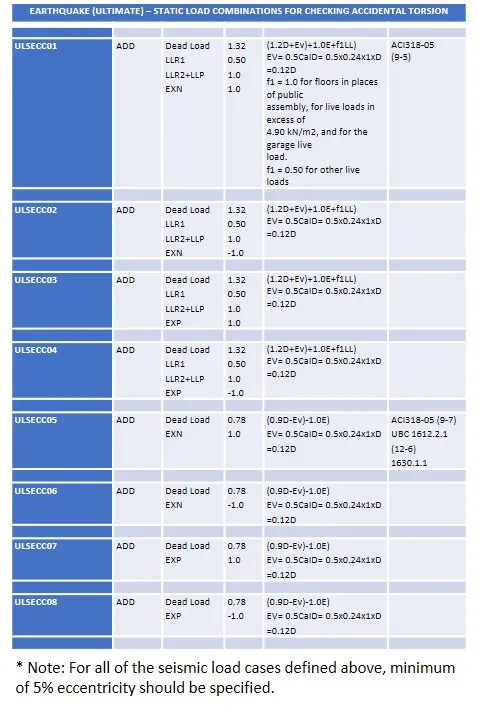Load combinations for seismic story shear along X. By yours truly.

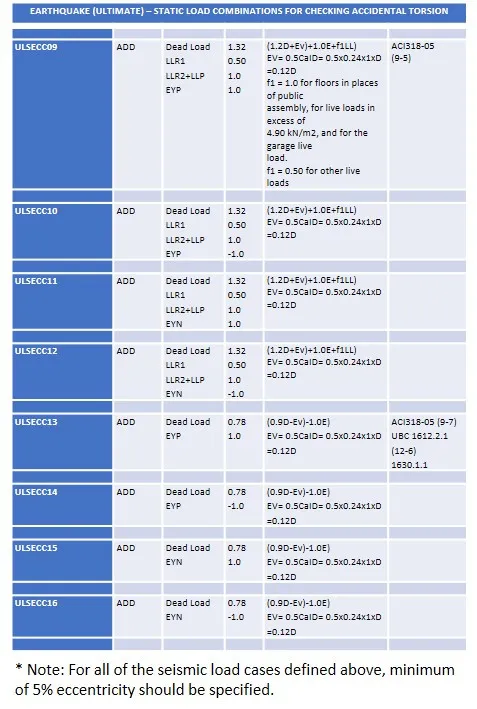Load combinations for seismic story shear along Y. By yours truly.

You might be tempted to use orthogonal load combinations of 1+0.30 but of course it does not make sense doing this because it would be like beating a dead horse. And needless to say that the additional 0.30 earthquake load from the orthogonal direction would produce unnecessary additional torsion when computing Ax (I know, I’ve said it anyway).

Now that we were finally able to define the related load combinations, we can now extract the displacements and proceed with the computation of torsional amplification factor Ax. To properly capture the torsional effects of which, let’s first assume that we have a rigid diaphragm (more on rigid and non-rigid diaphragms on the succeeding posts).

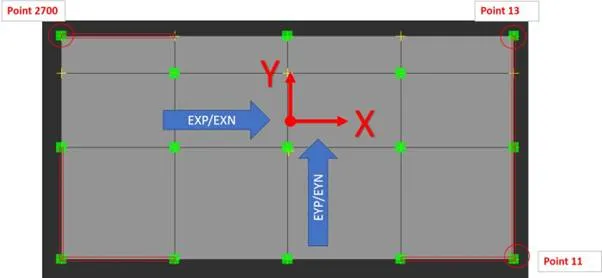sample model and snapshot by yours truly

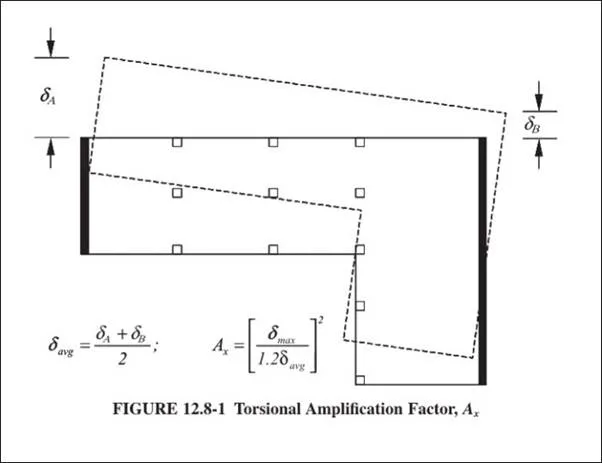cropped from ASCE7-10

For the story shear directed towards X, our control points where we are going to extract displacements are points 11 and 13. The story shear directed towards Y, our control points are points 13 and 2700. You can check this spreadsheet for the detailed calculation of the percentage of accidental eccentricity per load combo.

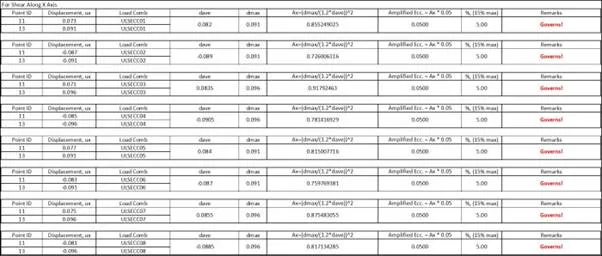For shear along X. by yours truly

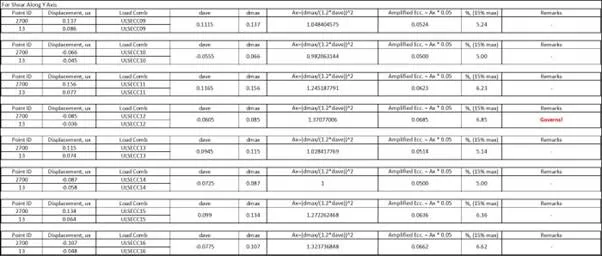For shear along Y. by yours truly

For the shear along X, we can see that no Ax exceeded unity, hence our amplified eccentricity remains 5% since we cannot reduce this value further as stipulated in the code. For the shear along Y however, with the load combination ULSECC12, the computed Ax is 1.37 and the resulting amplified accidental eccentricity is 6.85%. Elsewhere, no Ax exceeded 3.0 so there is no need for the accidental eccentricity to be at a maximum of 15%.

Note that we need to perform this computation per floor, and per diaphragm if one floor consists of several diaphragms. If you’re in a hurry however, you can provide the maximum computed eccentricity to all the diaphragms, that is if you’re ok with the overdesign. But since we’re aiming for an efficient and cost-effective design, we need not exceed the permitted maximum allowable.

It’s one thing to compute the eccentricity but how do we input this back to ETABS? In the Seismic Load Pattern dialogue box, inside the Overwrite Eccentricities, we can find a dialogue box where we can input the Story, the diaphragm label and the corresponding absolute length which is a function of Ax multiplied by the 5% eccentricity. For our example, the eccentricity of 36m*5%*1.37 = ±2.466m should be provided for both EYP and EYN. You were able to follow, right?

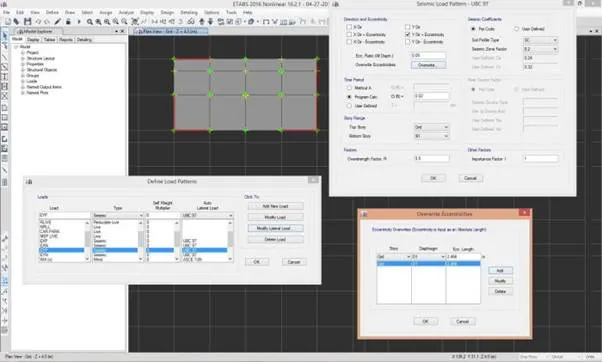snapshot from ETABS

I just wish to make a few more reiterations: just in case you are tempted to think that this accidental eccentricity is the total eccentricity, well, fact is it’s not. The point of application of a seismic story shear is at the center of mass such that the accidental eccentricity applies relative to this center of mass. And what some of us may not be aware of is that there is an eccentricity coming from the difference of the center of mass and center of rigidity which is computed internally in ETABS. So the total eccentricity is the inherent eccentricity e, plus/minus the accidental one. You might want to refer to CSI’s knowledge base and SEAOC’s Seismic Design Manual Volume 1 for much detailed examples.

Finally, let us relate seismic drift and accidental torsion.

Fact is, you have to first establish the torsional amplification factors before checking the drift. You cannot just sit pretty relaxed and contented that your drift values are within the prescribed limits while you’re still oblivious to the additional torsional moments that can be brought about by Ax greater than 1. Now it depends whether you have a rigid diaphragm or (behaving like rigid at least) before you can see its actual effects. Yes it’s that complicated.

So remember to first compute the torsional amplification factors before checking the drift!