Rotating Spectral Axes

(Before anything else, I would like to acknowledge our design manager Dale who unselfishly shared this to everyone and some of my colleagues who accommodated my queries so that I can understand the concept enough for me to execute this in ETABS and finally write this here for all of you.)

No I’m not referring to any ancient magical weapon of any sort.

Going through bits and pieces of dynamic analysis, the natural frequency is related to the lumped mass per floor and the stiffness of the system with respect to translation in both horizontal directions.

If you can kindly read dynamic analysis textbooks because I’m no longer familiar with those (although I am thinking of refreshing myself with those concepts once more. Something to add to my to do list.) for an in-depth understanding of which then please do so.

But what is the significance for us in rotating the spectral axes? Remember that we need to balance the static base shear to the dynamic base shear, and that the period and the corresponding base shear on a particular angle must match. So if you’re using the dynamic load case and you don’t correct the angle, chances are you’re pumping incorrect forces to your building.

With the significance established, let me ram down our throats some basic concepts so that we can fully grasp this spectral axes rotation. Ready?

Given the mass and the stiffness, the building will vibrate at some point where the mass and the stiffness will tell it to vibrate. More like the building has a behavior of its own to which we have really no choice but to let math do its course.

The X-Y orientation to which we oriented our building MAY NOT be the exact direction that the building will vibrate. So don’t trouble yourself trying to compel it like making a canine do its tricks because it has a mind of its own.

Static base shear will not dictate this direction of vibration because like the equation for base shear in UBC 97, building period T is based on the building height and the parameter Ct whereas the exact period is based on its dynamic properties.

For a building with regular framing, we can expect that the first two mode of vibrations are translations (meaning it is either will sway first along X and then sway to Y direction for the second sway and the third is the torsion or twisting mode. But then again this is not absolute ok? I tell you this is only for relatively regular buildings)

Don’t forget to define the mass source, which is the mass that it will lump and will be used for the dynamic analysis.

With item 1 in mind, we can generate the response spectrum analysis through ETABS. Let’s try to analyze the modal mass participation table below of a sample model and see what the printed digits mean.

The modal mass participating ratios table

Row 1 indicates the information about the first mode of vibration which, incidentally is the vibration corresponding to the X direction (this does not coincide with the global X axis; you will see later why). How’s that? The largest participating mass ratio along UX (4th column) which is 0.609 occurs on the first mode. Hence, it earns the title of primary mode of vibration of translation along X.

Row 3 shows the translation corresponding to the Y direction (again, this does not coincide with the global Y axis). How’s that? The largest participating mass ratio along UY (5th column) which is 0.4619 occurs on the third mode so it earns the title of third mode of vibration of translation along Y.

Why skip the second mode? This doesn’t have anything to do with the spectral axes but it is worth mentioning that even though the mass participations UX and UY are less than the first and third mode or perhaps the other modes, if we go and have a look at column 12 which is RZ, we can see that it has the highest ratio. RZ corresponds to the torsion.

So if we summarize the dynamic behavior of the building we can conclude that:

The first mode is translation along X

The second mode is torsion

The third mode is translation along Y

I’ve read somewhere, sorry but I can’t remember where, that the ideal building behavior is first two modes should be translation and that torsion should come after that. If it was in a rather different order, then you might have some problems, not enough to say that the building is unstable or unsafe, but to say that the building behaves rather odd.

Pardon me for digressing a bit.

Just remember that the period where the greatest percentage of mass is swayed is the fundamental period of the structure in that particular direction.

So how do we know the angle on how much are we going to rotate our models?

There are two ways: first is by looking at the modal base reactions and the modal direction factors. Let us first determine the angle using the first method and use the second for validating our calculations.

Base Reactions

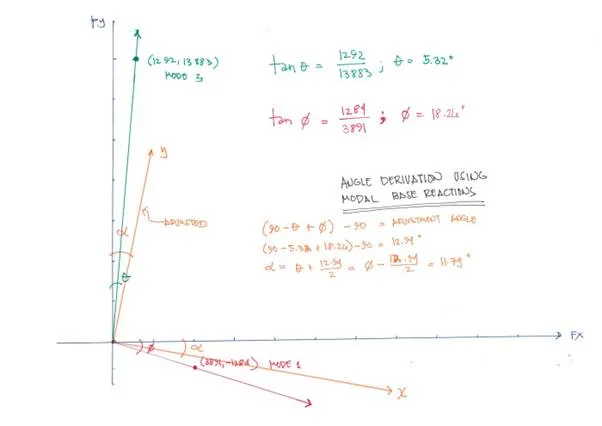Deriving rotation angle via modal base reaction

Taking the first mode reactions, we can get a triangle and the angle that it makes with the horizontal which is 18.26 degrees. This is the direction where 60.90% of the mass is engaged or is being displaced in this direction. Similarly for the third mode, we can get the angle that it makes with the vertical which is 5.36 degrees where 46.19% of the mass is engaged in that particular direction.

Now let’s validate this using the modal direction factors. You can see the modal direction factors which is part of the modal results by extracting the modal direction factors table. This is a bit tricky so pay close attention to how they are derived.

Deriving rotation angle via modal direction factors

The UX and UY therein are not vector quantities but scalar. We can read it rather this way: for mode 1, the building vibrates in a direction 18.36 degrees clockwise from the horizontal. Since it is angled, the resolved forces and displacements on the global x and y axes both have their effects on the direction of vibration. Again for mode 1, the effect of the forces along X is 0.827 along the direction of motion and add to this the contribution along Y which displaces it further by 0.091, still on the said direction of motion. You got the picture? We then apply the same principle to mode 3.

Whether we’re using the modal base reactions or the modal direction factors, we should arrive at the same computed angle.

Now what’s this adjusted angle? Ideally, the principal directions of translations should be orthogonal or normal to each other. But since this is not the case for modes 1 and 3, we need to adjust it such that the angle between the said directions are 90 degrees. You can actually adjust it closer to one derived axis but in the absence of related literature, what we do is we divide it evenly to make them meet halfway and hence the adjusted angle of 11.79 degrees clockwise.

So we finally derived the angle, it’s now time to make sure that the dynamic base shear along this corrected angle will not be less than 100% of the static base shear (that is if you’re not using ASCE which allows you to bring it down to 85%). How do we do it? We just need check the scale factors and the resulting spectral base reactions, resolve them vectorially to coincide with the computed axes and there you go.

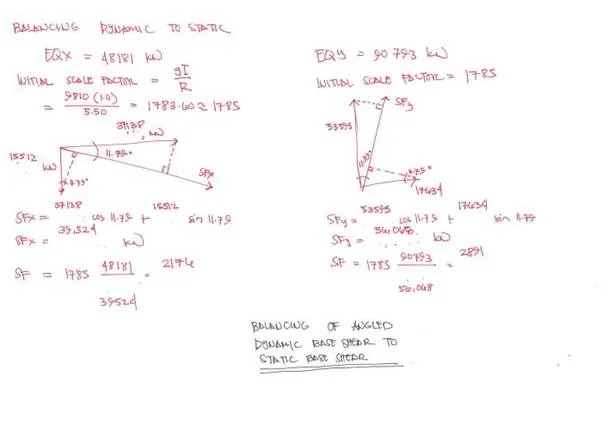Balancing static and angled dynamic base shearSpecx load case data. Note the angle and scale factor provided.Specy load case data. Note the angle and scale factor provided.

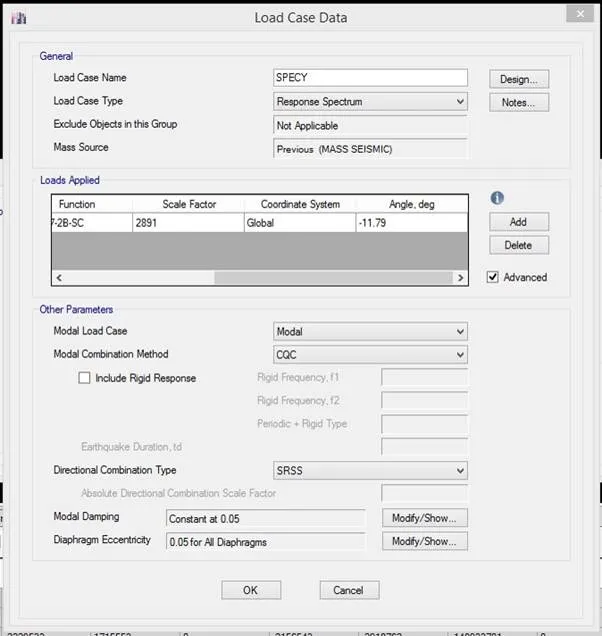SpecY load case definition

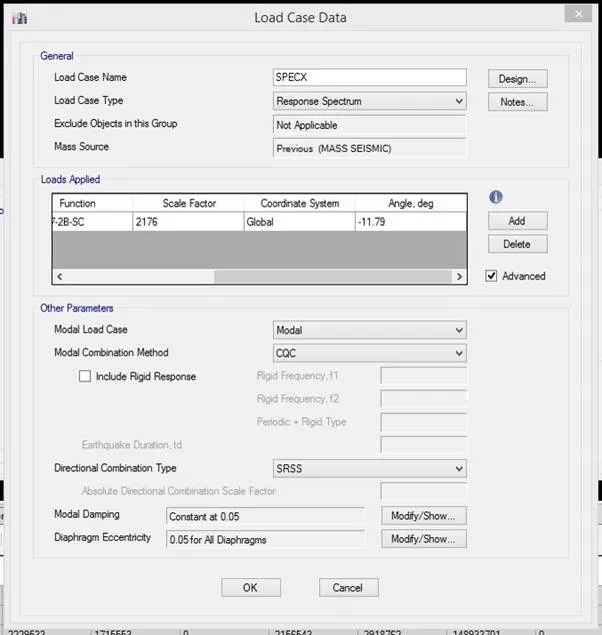SpecX load case definition

Another way of correcting the angle is by rotating the model in such a way that the correct directions of primary translations will coincide with the global axes. This we have done also in the past. So if this procedure will be followed, one must ensure that the modal base shears, the modal direction factors and modal mass participations should coincide with the global axes. How do we know that we already arrived on such conditions by looking at the digits mentioned above? I’ll leave it to you to figure out how or you can hit the comment section if you’re not sure how.

If you’re going to ask me the comparison of these two methodologies, then just like you I haven’t messed with it that much yet. But whatever the result is, I believe that it’s something worth digging for in the future.