Simplified Analysis of Continuous Beams

The analysis of continuous beams and frames to determine the bending moments and shear is an essential step in the design process of these members. Furthermore, the evaluation of the

maximum  deflection  is  a  mandatory  step  in  checking  the adequacy of  the design. There are many  computer  programs available to perform these tasks. However, a hand spot checks

for moments  at selected points still  necessary. Also, a quick determination  of  moments,  even  they  are  approximate,  is usually  required  for  simple  structures  and  preliminary

evaluation of complicated ones. The aim of the present work, is  to develope  a simple  and reasonably  accurate method  to determine moments and deflection for continuous beams. The

slope-deflection  method  and  a  beam  analysis  code  are implemented to analyze a large number of continuous beams of equal spans length. Beams of various span numbers and loading

distribution are investigated.  The method  of superposition is used to represent a continuous beam by the appropriate single-span beams (each span by two propped  cantilevers and  one

simply supported beam). Simple expressions are presented to determine the equivalent load on each of the substituent beams. From which, the bending moment, shear force and deflection at

any location can be calculated by the method of superposition. The validity of the suggesetd method are examined by applying it to several cases of contionuous beams. The presented method is found to give exact values for beams of two and three spans. While for the purpose of simplicity and getting compact  expressions, approximate  results with errors less than 0.5% are obtained for beams of four and more spans.

Keywords:  Continuous  beams,  closed-form  solution, structural analysis, equivalent single span beams, approximate bending moment.

INTRODUCTION

In  both  of the  analysis  and  design processes  of  continuous beams,  it  is  of  significant  importance  to  find  the  bending moment  and  deflection.  Therefore,  different  methods  are

developed to achieve  this aim. Some  of these methods yield exact values, but they usually involve extended mathematical operations.   On the other hand, others use simple formulas, but

approximate  values  are  obtained.  The  current  practice  of structural engineering uses the computer-aided analysis codes including  finite  element  method  to  analyze  complicated

statically indeterminate structures, which when skillfully used, can  give  almost  exact  results.  However,  the  use  of  simple approximate methods still necessary in many cases  as a  spot

check tool for checking the results of computer codes and for obtaining approximate values of the member forces, which are necessary  for the  preliminary  analysis, used  to  estimate  the

initial member sizes to be used in rigorous extensive analysis. More explanations about the reasons of the importance of the approximate methods of  structural analysis  are explained  by

McCormack.  

Benscoter developed an iterative method to determine the bending moments at internal supports of the continuous beams. His method started at first by representing each span by a single

span simply supported beam. Then the end slopes at the simple supports  together  with  the  flexibility  of  each  span  are determined.  The  next  step  is  to  determine  the  rotation

dislocation, which is the difference between the end slopes of the  adjacent  spans  at  their  common  supports.  The bending moment  at each  internal  support of the  continuous beam  is

proportional  to  the  value  of  the  angular  dislocation  at  that support and  the stiffness values of the two spans on its  both sides. The value of the bending moment at the internal support

of each span is then modified due to the carryover moment from the bending moment of the other internal support of the same span. The final step is to continue in iterations like that used in

the Hardy Cross moment distribution method developed  a  closed  form  analysis to  determine  the  support bending  moments  for  symmetric  continuous  beams.  His analysis  adopted  the  conjugate  beam  method  to  derive expressions for the span end moments, which depends on the ratio of the length of the loaded span to that of the considered span and the number of spans between them. The method was mainly devoted to the analysis of continuous highway bridge beams. In his paper, Harrison [5] presented a simplified finite element program that can be executed on a microcomputers to analyze plane frames and continuous beams.  The software can implimented  to determine  the bending  moments,  deflection, and draw the influence lines. The continuous beam can be of variable  cross-section  and  subjected  to  point or  trapezoidal distributed  load..  Jasim  and  Karim  [6]  used  moment distribution  method  to  derive  closed-form  expressions  to determine  the  exact  values  of  member  end  moments  of continuous  beams and  frames. The  method  is  based on  the series solution of the moment distribution terms obtained from the  successive  iterations.  The  final  expressions  need  no iteration and can be used irrespective of the type of loading. Dowell [7] suggested a method that can be used as a spot-check tool  to  determine  the  exact  member-end-moments  for continuous beams and bridge  structures. The method is  also based on the series  solution of  the distributed  moments and carry over factors. Dowell and Johnson [8] extend the closed from solution of continuous beams and bridge frames to include deep  beams  to  take  into  consideration  the  effect  of  shear deformation.  Series and  multiple products  expressions were used to find exact results as those obtained by stiffness method. Adam  et al  [9] used  the method  of  moment distribution  to analyze  continuous  beams  of various  number  of  spans  and different span lengths subjected to a uniformly distributed load on all spans. They determined the values of negative bending moments and the results were filtered and presented in tables and charts giving the  values of  coefficients for  the negative moments. The discrepancy of the results from the exact values may be up to about 9%. In other work, Adam [10] summarizes the bending moment values at supports of continuous beams in a form of charts. Beams of up to four spans with a uniformly distributed load and different length of spans were considered. There are also many other attempts to formulate closed-form solutions  for  the  analysis  of  cases  of  continuous  beams subjected  to vibration,  beams stiffened  with FRP, and skew curved beam.

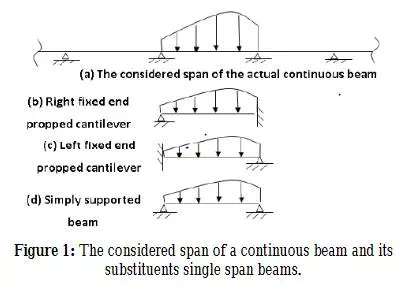
[11, 12, 13] The present work is an attempt to make use of the results of the exact  methods  of  analysis  to  derive  formulas,  although approximate, but simple to be used for preliminary analysis and design purposes. For this aim, the method of superposition of Jasim  and Atalla  [14],  which  was originally  developed,  for continuous  composite  beams  is  generalized  to  include  any continuous beam. In this method, each span of the continuous beam  is  substituted  by  three  single-span  beams,  namely; propped  cantilever  having  right  end  fixed  (RP),  propped cantilever  having  left end  fixed (LP),  and simply supported beam (SS). Each of these substituted single span beams, has the same length as that of the actual considered span, as described in Fig.(1). The load on the substituent two propped cantilever beams are  determined such that the  bending moments at  the fixed ends of RP and LP equal to the bending moment at the right and left supports of the considered span, respectively. Since the bending moments at the two supports of any span in a continuous beam are functions of the loads on all spans, thus,

the loads on the propped cantilevers are also functions of the loads on all spans of the continuous beam and not only of the considered span alone. The load on the third substituent beam,

i.e. the simply supported beam is determined such that the sum of the loads on the three substituent beams equals the load on the actual considered span.  It is worth to note that for any continuous beam,  the bending moment at the fixed  end of RP for  any span must  equal the bending moment at the fixed of LP of the next adjacent right span. This is because that the bending moments in their fixed supports must equal the bending moment in the actual common support between the considered spans of the continuous beam. Furthermore, it is obvious that the bending moment in LP for the first left span as well as the bending moment in RP for the last right span must be zero, since the moments at the exterior

supports are zero.