REQUIREMENT OF COMPATIBILITY CONDITIONS

 A direct determination of the six stress components requires six equations—three equilibrium equations and three compatibility conditions. However, indirect methods can be obtained by transforming stress into displacement or scalar function. The indirect methods emphasize either equilibrium equations or compatibility conditions. However, confirming the accuracy of the response generated by the direct or indirect methods requires satisfying the EE and the CC. Likewise, analysis of indeterminate structures requires both equilibrium and compatibility. The requirement of compatibility is illustrated by considering both Navier’s table problem for structures and a composite circular plate in elasticity.

Navier’s Table Problem

 Navier attempted to determine the four reactions (R1, R2, R3, and R4) along the legs of the table shown in Fig. 2. The symmetrical table is made of wood, rests on a level stone floor, and is subjected to a load P with eccentricities ex and ey. The table height is ø, and the distances between the legs along the x and y directions are 2a and 2b, respectively. Young’s modulus of the table leg material is E, and its cross-sectional area is A. The table top is considered rigid. The IFM solution for the four reactions is obtained by augmenting Navier’s three equilibrium equations with one compatibility condition:

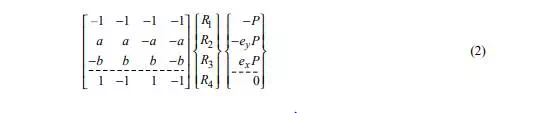
Solving the IFM equation yields the four reactions as follows

Composite Circular Plate

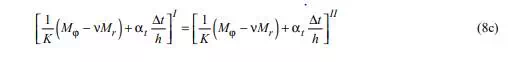
GENERATION OF COMPATIBILITY CONDITIONS