Collapse Mode

Since we don't know the relative values of H and V, we cannot determine the correct collapse mode. However, we can identify these collapse modes if we plot the three load factor equations derived above on the following interaction chart:

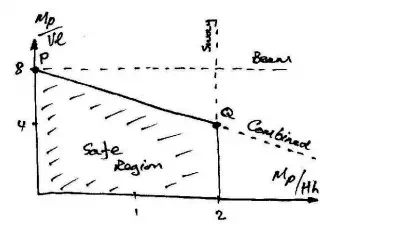
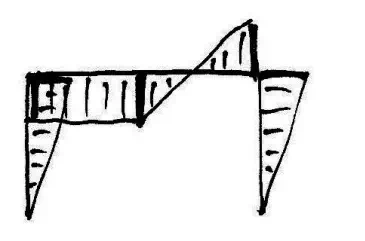
Notice that each mechanism defines a boundary and that it is only the region inside all of these boundaries that is safe. Now, for a given ration of V to H, we will be able to determine the critical collapse mechanism. Note also that the beam collapse mechanism is only critical for this frame at point P on the chart- this point is also included in the Combined mechanism. The bending moment diagrams corresponding to each of the mechanisms are approximately:

An interesting phenomenon is observed at point Q on the chart, where the Sway and Combined mechanisms give the same result. Looking at the bending moment diagrams, we can see that this occurs as the moment at the top of the left column becomes equal to the mid-span moment of the beam:

Upper bound (Unsafe) Theorem:

This can be stated as:

If a bending moment diagram is found which satisfies the conditions of equilibrium and mechanism (but not necessarily yield), then the corresponding load factor is either greater than or equal to the true load factor at collapse.

This is called the unsafe theorem because for an arbitrarily assumed mechanism the load factor is either exactly right (when the yield criterionismet) or is wrong and is too large, leading a designer to think that the frame can carry more load than is actually possible.

Lower bound (Safe)Theorem:

If a bending moment diagram is found which satisfies the conditions of equilibrium and yield (but not necessarily that of mechanism), then the corresponding load factor is either less than or equal to the true load factor at collapse