Definition of a Prismatic Beam

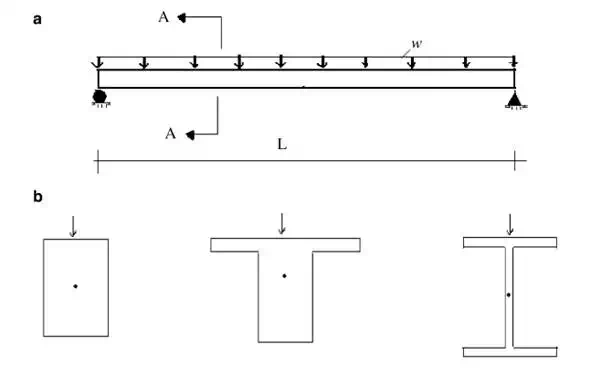
Beams are used extensively in structures, primarily in flooring systems for buildings and bridges. They belong to the line element category, i.e. their longitudinal dimension is large in comparison to their cross-sectional dimensions. Whereas truss members are loaded axially, beams are loaded normal to the longitudinal direction, and carry the loading by bending and twisting action. This mode is illustrated in Fig. 3.1. The transverse loading produces transverse deflection, which results in a nonuniform distribution of stress throughout the body.

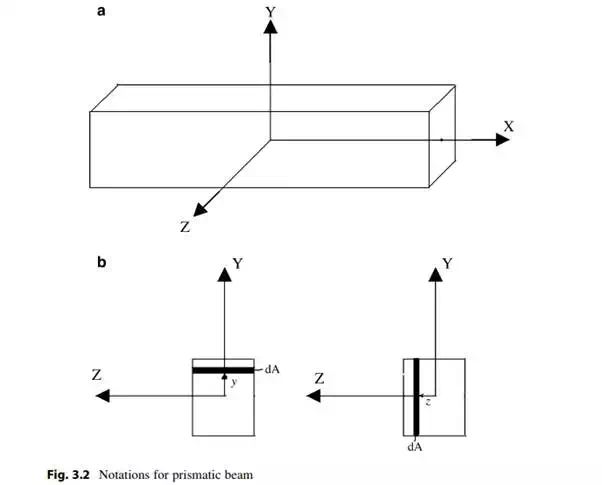
Most of the applications of beams in building structures involve straight beams with constant cross-section. We refer to this subgroup as prismatic beams. Figure 3.2 defines the geometrical parameters and notation used for prismatic beams. The longitudinal axis passes through the centroid of the cross-section, and the y, z axes are principal inertia directions. The relevant definition equations are

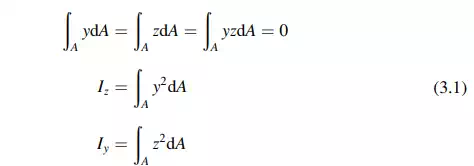
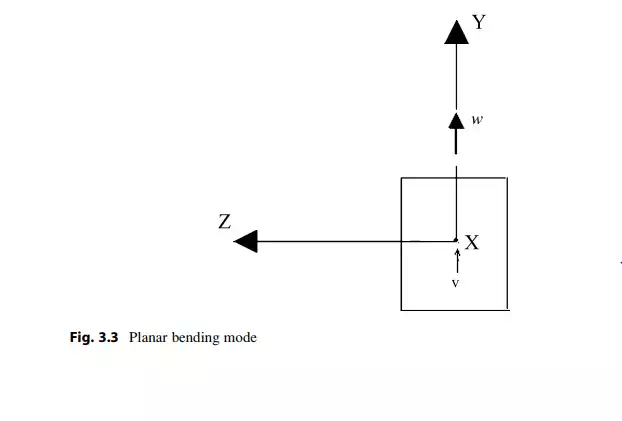
These conditions ensure that when the applied loads are in the x–y plane, points on the longitudinal axis will not displace in the z direction. Figure 3.3 illustrates this mode of behavior. For this type of loading, the longitudinal axis becomes a curve n(x) contained in the x–y plane. This type of behavior is called planar bending.

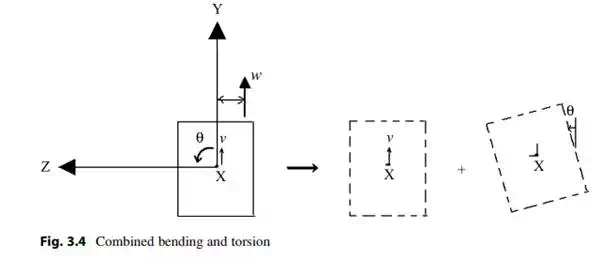
There are cases where the line of action of the loading does not pass through the X-axis, such as illustrated in Fig. 3.4. The eccentricity produces a torsional moment about the Z-axis, and the cross-section will rotate as well as deflect. This behavior is called “combined bending and torsion.” A prismatic member acted upon by just a torsional moment will experience only torsional behavior, i.e., the cross-section will just twist.

Mechanics of Solids texts deal with stresses and strains in beams. Our objective here is not to redevelop this material but rather to utilize it and formulate a structural theory for beams that will provide the basis for analyzing the behavior of structures composed of beam elements. Since structural theory is founded on Engineering Mechanics Theory, at least one subject dealing with Engineering Mechanics is usually required before studying Structural Theory. We assume that the reader has this level of exposure to Engineering Mechanics.