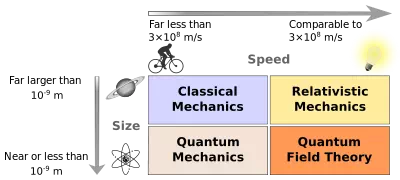
Classical Mechanics vs Quantum Mechanics

In this universe there are huge objects like planets and stars. There are also sub-atomic particles like protons and neutrons. You may note that at sub-atomic sizes, the wave nature of particles cannot be neglected and that the particles move at very high speeds. Which theory of Physics explains satisfactorily the behavior of both? Classical theory propounded by Issac Newton? Or General theory of relativity given by Einstein? This post is an introductory article before our in-depth analysis of Standard Particle Model of Quantum Mechanics.

Classical Mechanics for Macroscopic Objects

Classical mechanics describes the motion of macroscopic objects such as spacecraft, planets, stars, and galaxies. The classical mechanics (as known as Newtonian mechanics) provides extremely accurate results as long as the domain of study is restricted to large objects and the speeds involved do not approach the speed of light. The classical theories are simple, but this branch of mechanics cannot be applied to extremely small particles moving at very high speed, as the results may turn inaccurate.

Quantum Mechanics for Micro (and macro) scopic Objects

Quantum Mechanics has much more complicated theories than classical mechanics (thanks to Einstein), but provides accurate results for particles of even very small sizes. Quantum Mechanics handles the wave-particle duality of atoms and molecules. Special theory of relativity by Einstein (1905) deals with particles of extremely small sizes while General theory of relativity by Einstein (1916) can be used to study all particles in general, ie. even particles of macroscopic sizes. Thus it can be said that General theory of relativity is a super set of Special theory of relativity. But still Classical Mechanics is preferred to General theory of relativity for particles of macroscopic sizes, just because of its simplicity.

Standard Particle Model of Quantum Mechanics

One of the surprises of modern science is that atoms and sub-atomic particles do not behave like anything we see in the everyday world. They have wave properties, which is not observable in macroscopic objects. To describe this particular behavior, characteristics and interactions, scientists have developed a mathematical model known as Standard Particle Model. This model proposed two major groups of elementary particles of matter, ie. Quarks and Leptons. The model also proposed elementary force carriers known as Gauge Bosons and one Higgs Boson. Standard Particle Model links the matter-energy conversions, with the help of Quarks, Leptons, Gauge Bosons and Higgs Boson.

Beyond Standard Particle Model

The standard Particle model of Quantum mechanics is firmly set in the arena of special relativity, where the space-time background is flat. Defining particles in a fixed curved background space-time is not yet well-understood (except in some special cases).

Also, the proposed but not yet discovered particle Gravition, responsible for Gravitational force, does not come under the scope of Standard Particle Model.

Quantum Field Theory (QFT)

Statistical Mechanics at quantum level with many degrees of freedom: When both quantum mechanics and classical mechanics cannot apply, such as at the quantum level with many degrees of freedom, Quantum Field Theory (QFT) becomes applicable. QFT deals with small distances and large speeds with many degrees of freedom as well as the possibility of any change in the number of particles throughout the interaction. The scheme of Quantum Field Theory is that fermions interact by exchanging bosons. We will see more about Fermions and Bosons later.

To deal with large degrees of freedom at the macroscopic level, statistical mechanics becomes valid. Statistical mechanics explores the large number of particles and their interactions as a whole in everyday life. Statistical mechanics is mainly used in thermodynamics.

Non-Quantum Relativistic Mechanics vs Relativistic Quantum Mechanics vs Quantum Gravity

In physics, relativistic mechanics refers to mechanics compatible with special relativity (SR) and general relativity (GR). It provides a non-quantum mechanical description of a system of particles, or of a fluid, in cases where the velocities of moving objects are comparable to the speed of light c. As a result, classical mechanics is extended correctly to particles traveling at high velocities and energies, and provides a consistent inclusion of electromagnetism with the mechanics of particles. This was not possible in Galilean relativity, where it would be permitted for particles and light to travel at any speed, including faster than light. The foundations of relativistic mechanics are the postulates of special relativity and general relativity. The unification of SR with quantum mechanics is relativistic quantum mechanics, while attempts for that of GR is quantum gravity, an unsolved problem in physics.