IMPLEMENTATION OF RELIABILITY THEORY IN ENGINEERING ANALYSIS

Applications

The past two decades have seen a growth in the application of probabilistic risk assessment and reliability in numerous areas, including design code development and evaluation of critical facilities. Reliability-based structural codes

The gradual acceptance by standard writers of limit states design over the past two decades has made it possible to develop probability-based design procedures and common load requirements that can be used with different construction technologies. In several new standards in the United States, Canada and Western Europe, probabilistic methods have been used to take inherent variability and uncertainties in loads and structural strengths into account.

These advances in the technical basis for codes have been received enthusiastically by some groups; others, however, have been more reticent in their acceptance. Probability-based limit states design requires four basic types of information :12913

(1 ) a database to describe probabilities of occurrence and intensity of occupancy and environmental loads;

(2) probabilistic models of strength;

(3) models to describe the response of the structure; and

(4) procedures for computing the reliability measures (limit state probabilities or reliability indices) associated with various limit states for members, components or the system as a whole.

With this information, one can devise safety checking procedures based on prescribed target reliability levels. A structural system or component can be defined by its nominal (code-specified) material strength properties, dimensions and loads. These nominal design variables can be represented as

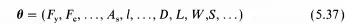
in which F,, Fc are strengths of steel, concrete or other material, A,, 1 are geometric parameters and D, L, W, S are dead, live, wind, snow or other loads. If the limit state G(X) < 0 is defined for a particular structure by 8 in terms of the (random) loads, strengths and dimensions, X, then Pf can be evaluated from Eq. (5.15) or P can be obtained from Eq. (5.17). Either way, the reliability of the structure can be analysed once the structure is defined by 8. In reliability-based design, the process is reversed. The code performance objective involving the design variables, 8, stated in probabilistic terms, is

in which Pro or Po are target limit state probability or reliability index set by the profession or by a regulatory authority. The goal of probability-based design is to define a structure, defined by nominal variables 8, through the use of a set of design equations of the form

in which Ri and Qj are nominal strengths and loads, and 4i and yj are resistance and load factors determined so that reliability goals of the code [expressed through Eqs (5.38)] are met, within limits, for all structures falling within the purview of the code. These load and resistance factors can be set by a mathematical optimization procedure that minimizes the squared deviation of P(8) from the target.