Compliance Control

Task strategy

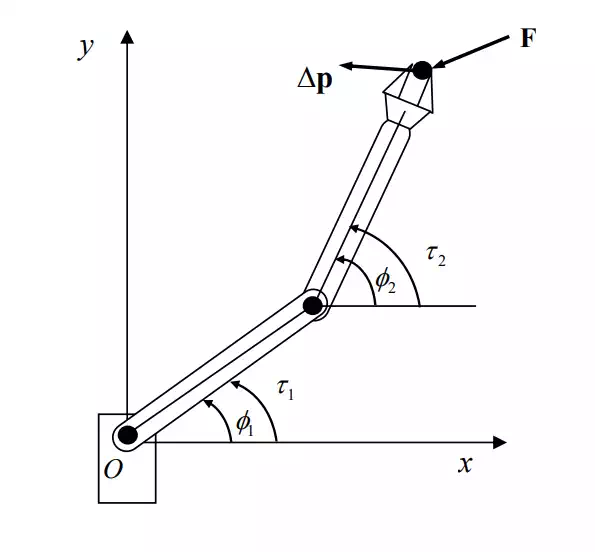
Use of both position and force information is a unique feature in the control of robots physically interacting with the environment. In hybrid position/force control, separation was made explicitly between position and force control loops through projections of feedback signals onto admissible motion space and constraint space. An alternative to this space separation architecture is to control a relationship between position and force in the task space. Compliance Control is a basic control law relating the displacement of the end-effecter to the force and moment acting on it. Rather than totally separating the task space into subspaces of either position or force control, compliance control reacts to the endpoint force such that a given functional relationship, typically a linear map, is held between the force and the displacement. Namely, a functional relationship to generate is given by

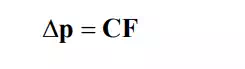
where C is an m x m Compliance Matrix, and ∆pand F are endpoint displacement and force represented in an m-dimensional, task coordinate system. Note that the inverse to the compliance matrix is a stiffness matrix:

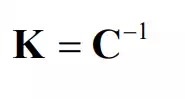
if the inverse exists.

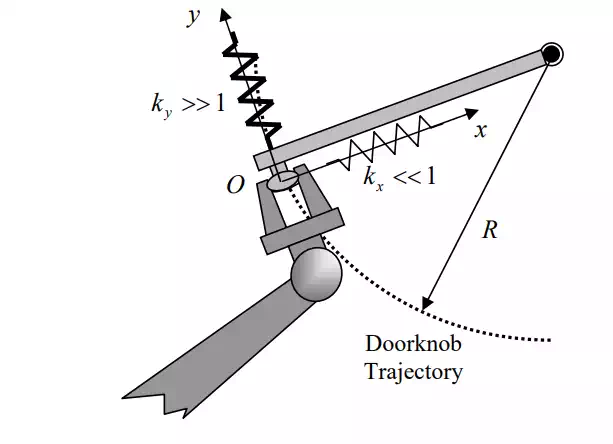
 The components of the compliance matrix, or the stiffness matrix, are design parameters to be determined so as to meet task objectives and constraints. Opening a door, for example, can be performed with the compiance illustrated in Figure 9.2.1. The trajectory of the doorknob is geometrically constrained to the circle of radius R centered at the door hinge. The robot hand motion must comply to the constrained doorknob trajectory, although the trajectory is not exactly known. The robot must not break the doorknob, although the conceived trajectory is different from the actual trajectory. This task requirement can be met by assigining a small stiffness, i.e. a high compliance, to the radial direction perpendicular to the trajectory. As illustrated in the figure,

such a small spring constant generates only a small restoring force in response to the discrepancy between the actual doorknob trajectory and the reference trajectory of the robot hand. Along the direction tangent to the doorknob trajectory, on the other hand, a large stiffness, or a small compliance, is assigned. This is to force the doorknob to move along the trajectory despite friction and other resistive forces. The stiffness matrix is therefore given by

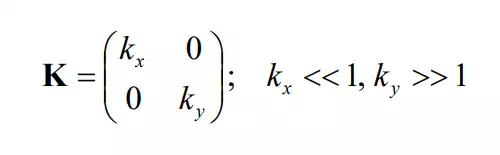
with reference to the task coordinate system O-xy. Using this stiffness with which the doorknow is held, the robot can open the door smoothly and dexterously, although the exact trajectory of the doorknob is not known.

Door opening with compliance control

Compliance control synthesis

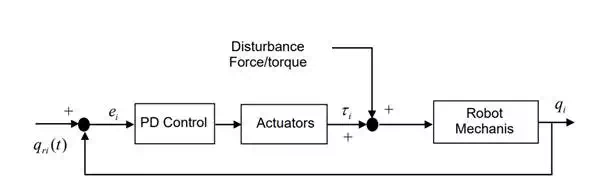
Now that a desired compliance is given, let us consider the method of generating the desired compliance. There are multiple ways of synthesizing a compliance control system. The simplest method is to accommodate the proportional gains of joint feedback controls so that desired restoring forces are generated in proportion to discrepancies between the actual and reference joint angles. As shown in Figure 9.2.2, a feedback control error is generated when a disturbance force or torque acts on the joint. At steady state a ststic balance is made, as an actuator torque i e i τ proportional to the control error cancels out the disturbance torque. The proportionality constant is determined by the position feedback gain ki, when friction is neglected. Therefore, a desired stiffness or compliance can be obtained by tuning the position feedback gain.

Compliance synthesis is trivial for single joint control systems. For general n degree-of freedom robots, however, multiple feedback loops must be coordinated. We now consider how to generate a desired m x m compliance or stiffness matrix specified at the endpoint by tuning joint feedback gains.

Single joint position feedback control system

Therefore, the obtained joint feedback gain provides the desired endpoint stiffness given by eq.(8), or the equivalent compliance.

Two link robots