Lagrangian Formulation of Robot Dynamics

Lagrangian Dynamics

In the Newton-Euler formulation, the equations of motion are derived from Newton's Second Law, which relates force and momentum, as well as torque and angular momentum. The resulting equations involve constraint forces, which must be eliminated to obtain closed form dynamic equations. In the Newton-Euler formulation, the equations are not expressed in terms of independent variables, and do not include input joint torques explicitly. Arithmetic operations are needed to derive the closed-form dynamic equations. This represents a complex procedure that requires physical intuition, as discussed in the previous section.

An alternative to the Newton-Euler formulation of manipulator dynamics is the Lagrangian formulation, which describes the behavior of a dynamic system in terms of work and energy stored in the system rather than of forces and moments of the individual members involved. The constraint forces involved in the system are automatically eliminated in the formulation of Lagrangian dynamic equations. The closed-form dynamic equations can be derived systematically in any coordinate system.

Let be generalized coordinates that completely locate a dynamic system. Let T and U be the total kinetic energy and potential energy stored in the dynamic system. We define the Lagrangian L by

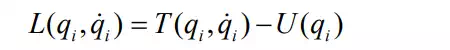
Note that the potential energy is a function of generalized coordinates qi and that the kinetic energy is that of generalized velocities as well as generalized coordinates qi. Using the Lagrangian, equations of motion of the dynamic system are given by

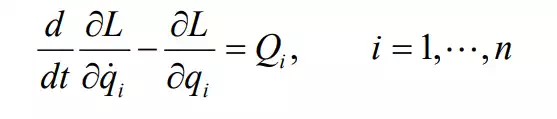
where Qi is the generalized force corresponding to the generalized coordinate qi. Considering the virtual work done by non-conservative forces can identify the generalized forces acting on the system.

Planar Robot Dynamics

Before discussing general robot dynamics in three-dimensional space, we consider the 2 dof planar robot, for which we have derived the equations of motion based on Newton-Euler Formulation. Figure 7.2.1 shows the same robot mechanism with a few new variables needed for the Lagrangian Formulation.

Two dof robot

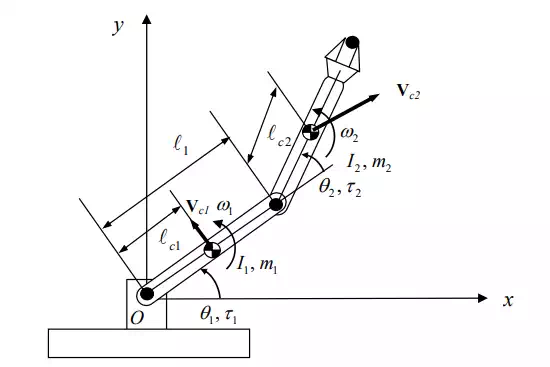
The total kinetic energy stored in the two links moving at linear velocity and angular velocity vci ωi at the centroids, as shown in the figur 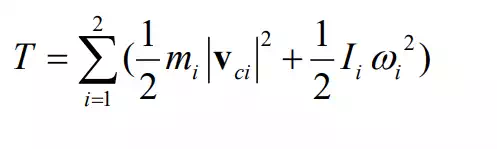 e, is given by

where vci represents the magnitude of the velocity vector. Note that the linear velocities and the angular velocities are not independent variables but are functions of joint angles and joint angular velocities, i.e. the generalized coordinates and the generalized velocities that locate the dynamic state of the system uniquely. We need to rewrite the above kinetic energy so that it is with respect to . The angular velocities are given by

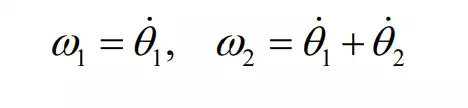
The linear velocity of the first link is simply

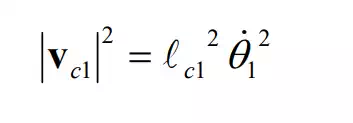
However, the centroidal linear velocity of the second link vc2 needs more computation. Treating the centroid C2 as an endpoint and applying the formula for computing the endpoint velocity yield the centroidal velocity. Let be the 2x2 Jacobian matrix relating the centroidal velocity vector to joint velocities. Then,

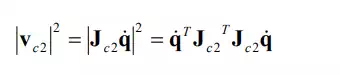
where ( . Substituting eqs.(4~6) to eq.(3) yields

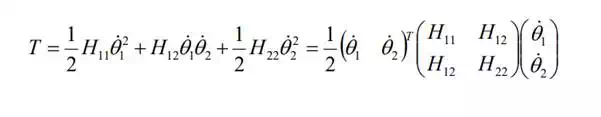
Substituting the above two equations into eq.(2) yields the same result as eq.(7.1.11-a). The equation of motion for the second joint can be obtained in the same manner, which is identical to eq.(7.1.11-b). Thus, the same equations of motion have been obtained based on Lagrangian Formulation. Note that the Lagrangian Formulation is simpler and more systematic than the Newton-Euler Formulation. To formulate kinetic energy, velocities must be obtained, but accelerations are not needed. Remember that the acceleration computation was complex in the Newton-Euler Formulation, as discussed in the previous section. This acceleration computation is automatically dealt with in the computation of Lagrange’s equations of motion. The difference between the two methods is more significant when the degrees of freedom increase, since many workless constraint forces and moments are present and the acceleration computation becomes more complex in Newton-Euler Formulation.