Physical Interpretation of the Dynamic Equations

 In this section, we interpret the physical meaning of each term involved in the closed form dynamic equations for the two-dof planar robot.

 The last term in each of eqs. (11-a, b), Gi , accounts for the effect of gravity. Indeed, the terms G1 and G2, given by (12-e, f), represent the moments created by the masses m1 and m2 about their individual joint axes. The moments are dependent upon the arm configuration. When the arm is fully extended along the x-axis, the gravity moments become maximums.

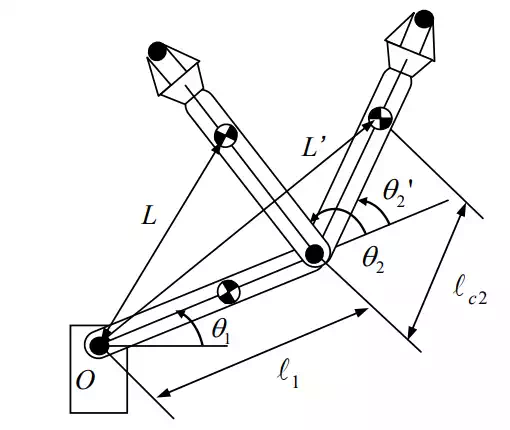
Next, we investigate the first terms in the dynamic equations. When the second joint is immobilized, i.e. , the first dynamic equation reduces to , where the gravity term is neglected. From this expression it follows that the coefficient H11 accounts for the moment of inertia seen by the first joint when the second joint is immobilized. The coefficient H11 given by eq. (12-a) is interpreted as the total moment of inertia of both links reflected to the first joint axis. The first two terms, , in eq. (12-a), represent the moment of inertia of link 1 with respect to joint 1, while the other terms are the contribution from link 2. The inertia of the second link depends upon the distance L between the centroid of link 2 and the first joint axis, as illustrated in Figure 7.1.3. The distance L is a function of the joint angle θ 2 = 0 and θ 2 = 0   1 11θ1 τ H = 1 2 1 1 m I A c + θ2 and is given by

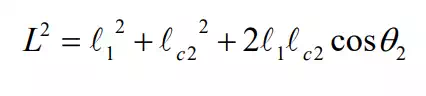
Using the parallel axes theorem of moment of inertia (Goldstein, 1981), the inertia of link 2 with respect to joint 1 is m2L2 +I2 , which is consistent with the last two terms in eq. (12-a). Note that the inertia varies with the arm configuration. The inertia is maximum when the arm is fully extended ( 0 θ 2 = ), and minimum when the arm is completely contracted (θ 2 = π ).

Varying inertia depending on the arm configuration

Let us now examine the second terms on the right hand side of eq. (11). Consider the instant when 1 2 1 , then the first equation reduces to 1 12 2 , where the gravity term is again neglected. From this expression it follows that the second term accounts for the effect of the second link motion upon the first joint. When the second link is accelerated, the reaction force and torque induced by the second link act upon the first link. This is clear in the original Newton-Euler equations (4), where the coupling force -fl,2 and moment -N1,2 from link 2 are involved in the dynamic equation for link 1. The coupling force and moment cause a torque θ = θ = 0 and θ = 0    τ θ H = int τ about the first joint axis given by

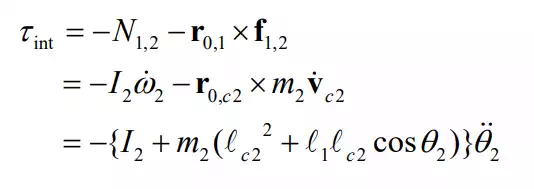
where N1,2 and fl,2 are evaluated using eq. (5) for 1 2 1 . This agrees with the second term in eq. (11-a). Thus, the second term accounts for the interaction between the two joints.

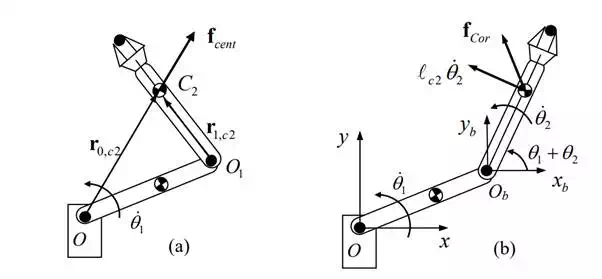
The third terms in eq. (11) are proportional to the square of the joint velocities. We consider the instant when 2 1 2. In this case, a centrifugal force acts upon the second link. Let fcent be the centrifugal force. Its magnitude is given by

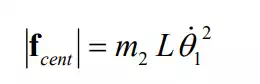
where L is the distance between the centroid C2 and the first joint O. The centrifugal force acts in the direction of position vector O,C2 r . This centrifugal force causes a moment τcent about the second joint. Using eq. (16), the moment τcent is computed as

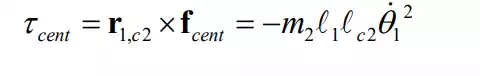
This agrees with the third term h 1 in eq. (11-b). Thus we conclude that the third term is caused by the centrifugal effect on the second joint due to the motion of the first joint. Similarly, rotating the second joint at a constant velocity causes a torque of due to the centrifugal effect upon the first joint.

Centrifugal (a) and Coriolis (b) effects

Finally, we discuss the fourth term of eq. (11-a), which is proportional to the product of the joint velocities. Consider the instant when the two joints rotate at velocities at the same time. Let Ob-xbyb be the coordinate frame attached to the tip of link 1. Note that the frame Ob-xbyb is parallel to the base coordinate frame at the instant shown. However, the frame rotates at the angular velocity together with link 1. The mass centroid of link 2 moves at a velocity of relative to link 1, i.e. the moving coordinate frame Ob-xbyb. When a mass particle m moves at a velocity of vb relative to a moving coordinate frame rotating at an angular velocity ω, the mass particle has the so-called Coriolis force given by . Let fCor be the force acting on link 2 due to the Coriolis effect. The Coriolis force is given by

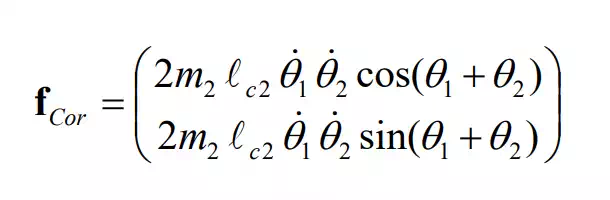
This Coriolis force causes a moment τ C or about the first joint, which is given by

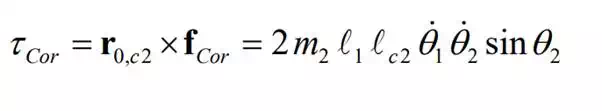
The right-hand side of the above equation agrees with the fourth term in eq. (11-a). Since the Coriolis force given by eq. (18) acts in parallel with link 2, the force does not create a moment about the second joint in this particular case.

 Thus, the dynamic equations of a robot arm are characterized by a configuration dependent inertia, gravity torques, and interaction torques caused by the accelerations of the other joints and the existence of centrifugal and Coriolis effects.