Dynamics

 In this chapter, we analyze the dynamic behavior of robot mechanisms. The dynamic behavior is described in terms of the time rate of change of the robot configuration in relation to the joint torques exerted by the actuators. This relationship can be expressed by a set of differential equations, called equations of motion, that govern the dynamic response of the robot linkage to input joint torques. In the next chapter, we will design a control system on the basis of these equations of motion.

Two methods can be used in order to obtain the equations of motion: the Newton-Euler formulation, and the Lagrangian formulation. The Newton-Euler formulation is derived by the direct interpretation of Newton's Second Law of Motion, which describes dynamic systems in terms of force and momentum. The equations incorporate all the forces and moments acting on the individual robot links, including the coupling forces and moments between the links. The equations obtained from the Newton-Euler method include the constraint forces acting between adjacent links. Thus, additional arithmetic operations are required to eliminate these terms and obtain explicit relations between the joint torques and the resultant motion in terms of joint displacements. In the Lagrangian formulation, on the other hand, the system's dynamic behavior is described in terms of work and energy using generalized coordinates. This approach is the extension of the indirect method discussed in the previous chapter to dynamics. Therefore, all the workless forces and constraint forces are automatically eliminated in this method. The resultant equations are generally compact and provide a closed-form expression in terms of joint torques and joint displacements. Furthermore, the derivation is simpler and more systematic than in the Newton-Euler method.

The robot’s equations of motion are basically a description of the relationship between the input joint torques and the output motion, i.e. the motion of the robot linkage. As in kinematics and in statics, we need to solve the inverse problem of finding the necessary input torques to obtain a desired output motion. This inverse dynamics problem is discussed in the last section of this chapter. Efficient algorithms have been developed that allow the dynamic computations to be carried out on-line in real time.

 Newton-Euler Formulation of Equations of Motion

Basic Dynamic Equations

 In this section we derive the equations of motion for an individual link based on the direct method, i.e. Newton-Euler Formulation. The motion of a rigid body can be decomposed into the translational motion with respect to an arbitrary point fixed to the rigid body, and the rotational motion of the rigid body about that point. The dynamic equations of a rigid body can also be represented by two equations: one describes the translational motion of the centroid (or center of mass), while the other describes the rotational motion about the centroid. The former is Newton's equation of motion for a mass particle, and the latter is called Euler's equation of motion.

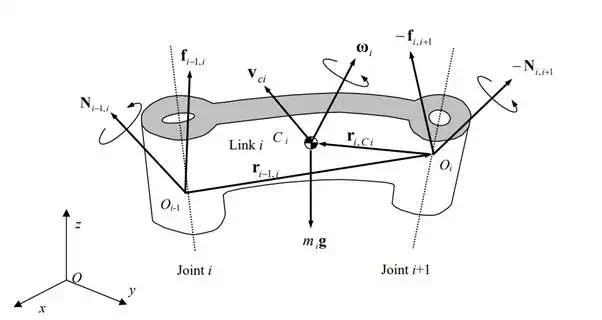
 We begin by considering the free body diagram of an individual link. all the forces and moments acting on link i. The figure is the same as, which describes the static balance of forces, except for the inertial force and moment that arise from the dynamic motion of the link. Let be the linear velocity of the centroid of link i with reference to the base coordinate frame O-xyz, which is an inertial reference frame. The inertial force is then given by , where mi is the mass of the link and is the time derivative of . Based on D’Alembert’s principle, the equation of motion is then obtained by adding the inertial force to the static balance of forces in eq.(6.1.1) so that

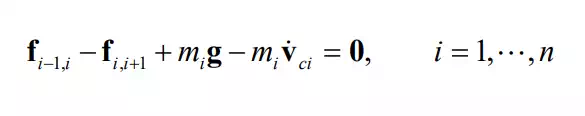
where, as in Chapter 6, are the coupling forces applied to link i by links i-1 and i+1, respectively, and g is the acceleration of gravity.

Free body diagram of link i in motion

Rotational motions are described by Euler's equations. In the same way as for translational motions, adding “inertial torques” to the static balance of moments yields the dynamic equations. We begin by describing the mass properties of a single rigid body with respect to rotations about the centroid. The mass properties are represented by an inertia tensor, or an inertia matrix, which is a 3 x 3 symmetric matrix defined by

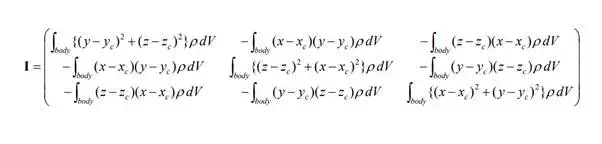
where ρ is the mass density, are the coordinates of the centroid of the rigid body, and each integral is taken over the entire volume V of the rigid body. Note that the inertia matrix varies with the orientation of the rigid body. Although the inherent mass property of the rigid body does not change when viewed from a frame fixed to the body, its matrix representation when viewed from a fixed frame, i.e. inertial reference frame, changes as the body rotates.

The inertial torque acting on link i is given by the time rate of change of the angular momentum of the link at that instant. Let be the angular velocity vector and be the centroidal inertia tensor of link i, then the angular momentum is given by . Since the inertia tensor varies as the orientation of the link changes, the time derivative of the angular momentum includes not only the angular acceleration term , but also a term resulting from changes in the inertia tensor viewed from a fixed frame. This latter term is known as the gyroscopic torque and is given by . Adding these terms to the original balance of moments (4-2) yields

using the notations of Figure 7.1.1. Equations (2) and (3) govern the dynamic behavior of an individual link. The complete set of equations for the whole robot is obtained by evaluating both equations for all the links, i = 1, · ,n.

Closed-Form Dynamic Equations

The Newton-Euler equations we have derived are not in an appropriate form for use in dynamic analysis and control design. They do not explicitly describe the input-output relationship, unlike the relationships we obtained in the kinematic and static analyses. In this section, we modify the Newton-Euler equations so that explicit input-output relations can be obtained. The Newton-Euler equations involve coupling forces and moments . As shown in eqs.(6.2.1) and (6.2.2), the joint torque τi, which is the input to the robot linkage, is included in the coupling force or moment. However, τi is not explicitly involved in the Newton-Euler equations. Furthermore, the coupling force and moment also include workless constraint forces, which act internally so that individual link motions conform to the geometric constraints imposed by the mechanical structure. To derive explicit input-output dynamic relations, we need to separate the input joint torques from the constraint forces and moments. The Newton-Euler equations are described in terms of centroid velocities and accelerations of individual arm links. Individual link motions, however, are not independent, but are coupled through the linkage. They must satisfy certain kinematic relationships to conform to the geometric constraints. Thus, individual centroid position variables are not appropriate for output variables since they are not independent.

 The appropriate form of the dynamic equations therefore consists of equations described in terms of all independent position variables and input forces, i.e., joint torques, that are explicitly involved in the dynamic equations. Dynamic equations in such an explicit input- output form are referred to as closed-form dynamic equations. As discussed in the previous chapter, joint displacements q are a complete and independent set of generalized coordinates that locate the whole robot mechanism, and joint torques τ are a set of independent inputs that are separated from constraint forces and moments. Hence, dynamic equations in terms of joint displacements q and joint torques τ are closed-form dynamic equations.

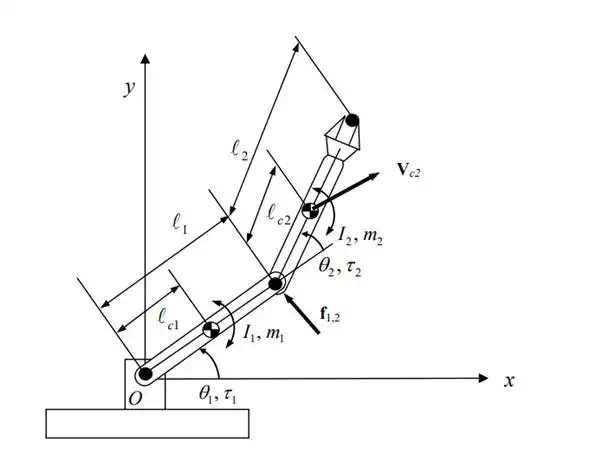
 The two dof planar manipulator that we discussed in the previous chapter. Let us obtain the Newton-Euler equations of motion for the two individual links, and then derive closed-form dynamic equations in terms of joint displacements 1 2 θ andθ , and joint torques τ1 and τ2. Since the link mechanism is planar, we represent the velocity of the centroid of each link by a 2-dimensional vector vi and the angular velocity by a scalar velocity ωi . We assume that the centroid of link i is located on the center line passing through adjacent joints at a distance from joint i, as shown in the figure. The axis of rotation does not vary for the planar linkage. The inertia tensor in this case is reduced to a scalar moment of inertia denoted by Ii.

From eqs. (1) and (3), the Newton-Euler equations for link 1 are given by

Note that all vectors are 2 x 1, so that moment N i-1,i and the other vector products are scalar quantities. Similarly, for link 2

Mass properties of two dof planar robot

To obtain closed-form dynamic equations, we first eliminate the constraint forces and separate them from the joint torques, so as to explicitly involve the joint torques in the dynamic equations. For the planar manipulator, the joint torques τ1 and τ2 are equal to the coupling moments:

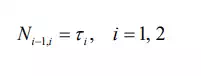
Substituting eq.(6) into eq.(5) and eliminating f1,2 we obtain

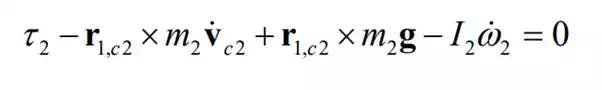
Similarly, eliminating f0,1 yields,

Next, we rewrite , 1 ci , i , and i i+ v ω r using joint displacements 1 2 θ and θ , which are independent variables. Note that ω2 is the angular velocity relative to the base coordinate frame, while θ2 is measured relative to link 1. Then, we have

The linear velocities can be written as

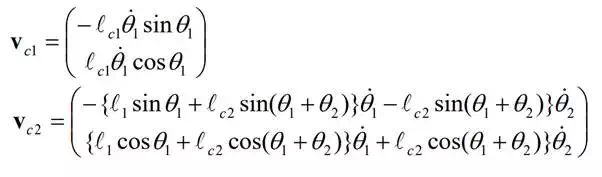
Substituting eqs. (9) and (10) along with their time derivatives into eqs. (7) and (8), we obtain the closed-form dynamic equations in terms of 1 2 θ andθ :

Where

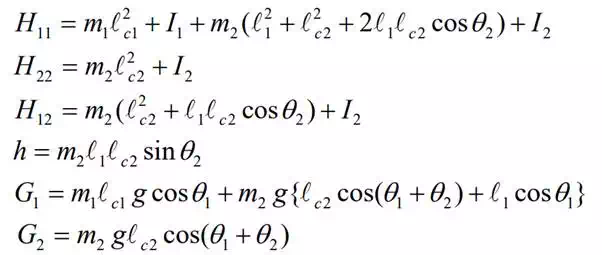
The scalar g represents the acceleration of gravity along the negative y-axis.

More generally, the closed-form dynamic equations of an n-degree-of-freedom robot can be given in the form

where coefficients Hij , hijk, and Gi are functions of joint displacements . When external forces act on the robot system, the left-hand side must be modified accordingly.