Duality of Differential Kinematics and Statics
We have found that the equivalent joint torques are related to the endpoint force by the Jacobian matrix, which is the same matrix that relates the infinitesimal joint displacements to the end-effecter displacement. Thus, the static force relationship is closely related to the differential kinematics. In this section we discuss the physical meaning of this observation.
To interpret the similarity between differential kinematics and statics, we can use the linear mapping diagram of Figure 5.4.1. Recall that the differential kinematic equation can be regarded as a linear mapping when the Jacobian matrix is fixed at a given robot configuration. reproduces and completes it with a similar diagram associated with the static analysis. As before, the range space R(J) represents the set of all the possible end-effecter velocities generated by joint motions. When the Jacobian matrix is degenerate, or the robot configuration is singular, the range space does not span the whole vector space. Namely, there exists a direction in which the end-effecter cannot move with a non-zero velocity. See the subspace S2 in the figure. The null space N(J), on the other hand, represents the set of joint velocities that do not produce any velocity at the end-effecter. If the null space contains a nonzero element, the differential kinematic equation has an infinite number of solutions that cause the same end-effecter velocity.
The lower half of is the linear mapping associated with the static force relationship given by eq.(6.2.4). Unlike differential kinematics, the mapping of static forces is given by the transpose of the Jacobian, generating a mapping from the m-dimensional vector space Vm, associated with the Cartesian coordinates of the end-effecter, to the n-dimensional vector space Vn , associated with the joint coordinates. Therefore, the joint torques τ are always determined uniquely for any arbitrary endpoint force F. However, for given joint torques, a balancing endpoint force does not always exist. As in the case of the differential kinematics, let us define the null space N(JT ) and the range space R(JT ) of the static force mapping. The null space N(JT ) represents the set of all endpoint forces that do not require any torques at the joints to bear the corresponding load. In this case the endpoint force is borne entirely by the structure of the linkage mechanism, i.e. constraint forces. The range space R(JT ), on the other hand, represents the set of all the possible joint torques that can balance the endpoint forces.
Duality of differential kinematics and statics
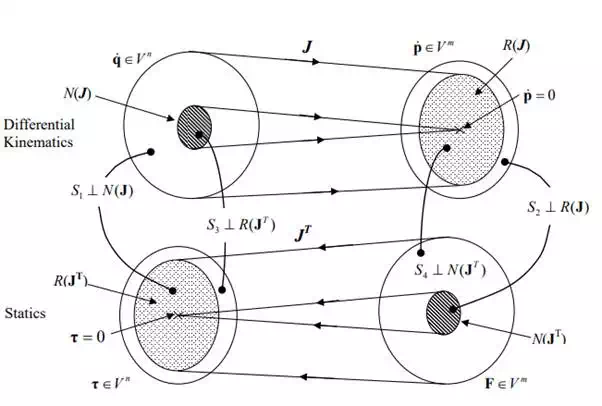
The ranges and null spaces of J and JT are closely related. According to the rules of linear algebra, the null space N(J) is the orthogonal complement of the range space R(JT ). Namely, if a non-zero n-vector x is in N(J) , it cannot also belong to R(JT ), and vice-versa. If we denote by S1 the orthogonal complement of N(J), then the range space R(JT ) is identical to S1, as shown in the figure. Also, space S3, i.e., the orthogonal complement of R(JT ) is identical to N(J). What this implies is that, in the direction in which joint velocities do not cause any end-effecter velocity, the joint torques cannot be balanced with any endpoint force. In order to maintain a stationary configuration, the joint torques in this space must be zero.
There is a similar correspondence in the end-effecter coordinate space Vm. The range space R(J) is the orthogonal complement to the null space N(JT ). Hence, the subspace S2 in the figure is identical to N(JT ), and the subspace S4 is identical to R(J). Therefore, no joint torques are required to balance the end point force when the external force acts in the direction in which the end-effecter cannot be moved by joint movements. Also, when the external endpoint force is applied in the direction along which the end-effecter can move, the external force must be borne entirely by the joint torques. When the Jacobian matrix is degenerate, or the arm is in a singular configuration, the null space N(JT ) has a non-zero dimension, and the external force can be borne in part by the mechanical structure. Thus, differential kinematics and statics are closely related. This relationship is referred to as the duality of differential kinematics and statics.
Closed-Loop Kinematic Chains
The relationship between joint torques and the endpoint force obtained can be extended to a class of parallel-link mechanisms with closed kinematic-chains. It can also be extended to multi-fingered hands, leg locomotion, and other robot mechanisms having closed kinematic chains. In this section we discuss classes of closed kinematic chains based on the principle of virtual work.
Five-bar-link robot exerting endpoint force
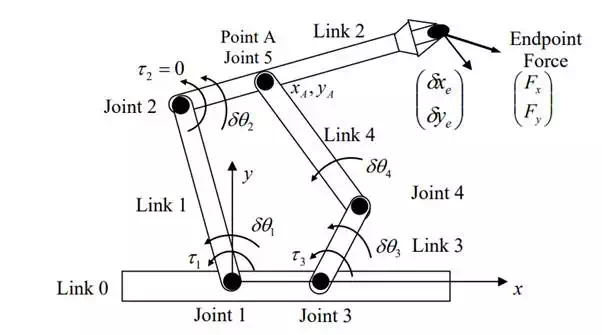
We begin by revisiting the five-bar-link planar robot shown
in Figure 6.4.1. This robot has two degrees of freedom, comprising two active
joints, Joints 1 and 3, and three passive joints, Joints 2, 4, and 5. Therefore
the virtual work associated with the endpoint force and joint toques is given
by 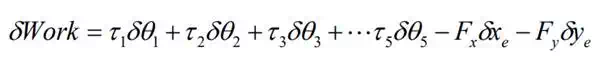
We assume no friction at the joints. Therefore, the three passive joints cannot bear any torque load about their joint axis. Substituting τ 2 = τ 4 = τ 5 = 0 into the above yields
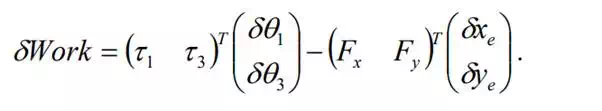
For any given configuration of the robot, the virtual displacements of the end-effecter are uniquely determined by the virtual displacements of Joints 1 and 3. In fact, the former is related to the latter via the Jacobian matrix:
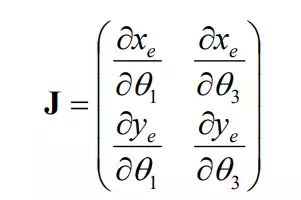
Using this Jacobian,

Note that the joint coordinates associated with the active joints are not necessarily generalized coordinates that uniquely locate the system. For example, the arm configuration of the five-bar-link robot is not uniquely determined with joint anglesθ1 and θ3 alone. There are two configurations for given θ1 and θ3 . The corollary requires the differential relation to be defined uniquely in the vicinity of the given configuration.
Over-Actuated Systems
If an n degree-of-freedom robot system has more than n active joints, or less than n active joints, the above corollary does not apply. These are called over-actuated and under-actuated systems, respectively. Over-actuated systems are of importance in many manipulation and locomotion applications. In the following, we will consider the static relationship among joint torques and endpoint forces for a class of over-actuated systems.
a two-fingered hand manipulating an object within a plane. Note that both fingers are connected at the fingertips holding the object. While holding the object, the system has three degrees of freedom. Since each finger has two active joints, the total number of active joints is four. Therefore, the system is over-actuated.
Using the notation shown in the figure, the virtual work is given by
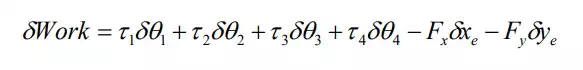
Note that only three virtual displacements of the four joint angles are independent. There exists a differential relationship between one of the joints, say θ 4 , and the other three due to the kinematic constraint. Let us write it as
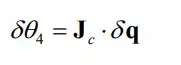

This gives a particular combination of joint torques that do not influence the force balance with the external endpoint load F. The joint torques having this proportion generate the internal force applied to the object, as illustrated in the figure. This internal force is a grasp force that is needed for performing a task.
Two-fingered hand manipulating a grasped object
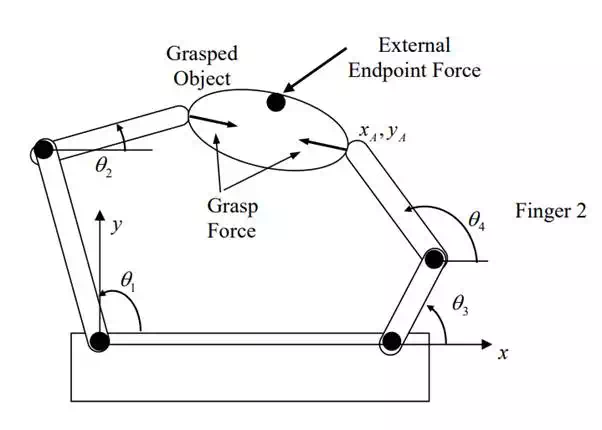
Define geometric parameters needed and obtain the two Jacobian matrices associated with the two-fingered hand holding an object. Furthermore, obtain the grasp force using the Jacobian matrices and the joint torques.