Properties of the Jacobian

The Jacobian plays an important role in the analysis, design, and control of robotic systems. It will be used repeatedly in the following chapters. It is worth examining basic properties of the Jacobian, which will be used throughout this book.

 We begin by dividing the 2-by-2 Jacobian of into two column vectors:

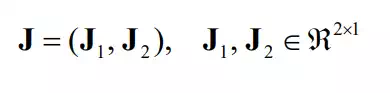
Then can be written as

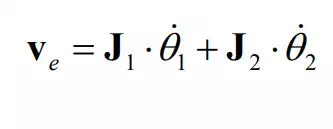
The first term on the right-hand side accounts for the end-effecter velocity induced by the first joint only, while the second term represents the velocity resulting from the second joint motion only. The resultant end-effecter velocity is given by the vectorial sum of the two. Each column vector of the Jacobian matrix represents the end-effecter velocity generated by the corresponding joint moving at a unit velocity when all other joints are immobilized.

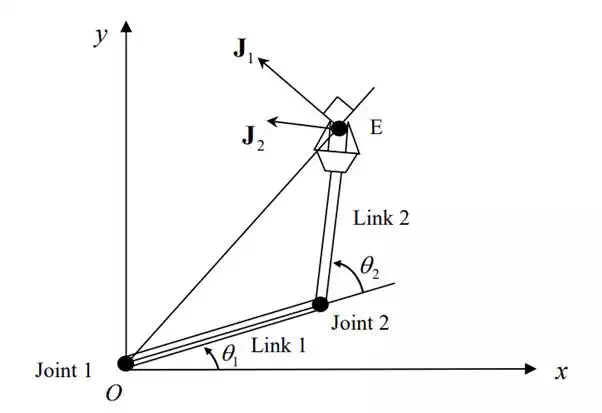
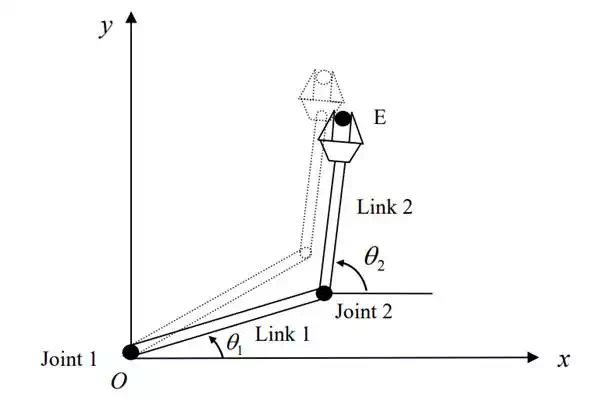
 Illustrates the column vectors 1 2 of the 2 dof robot arm in the two dimensional space. Vector 2 J , given by the second column of eq.(5.1. 8), points in the direction perpendicular to link 2. Note, however, that vector 1 is not perpendicular to link 1 but is perpendicular to line OE, the line from joint 1 to the endpoint E. This is because 1 represents the endpoint velocity induced by joint 1 when joint 2 is immobilized. In other words, links 1 and 2 are rigidly connected, becoming a single rigid body of link length OE, and is the tip velocity of the link OE.

Geometric interpretation of the column vectors of the Jacobian

In general, each column vector of the Jacobian represents the end-effecter velocity and angular velocity generated by the individual joint velocity while all other joints are immobilized. Letpbe the end-effecter velocity and angular velocity, or the end-effecter velocity for short, and Ji be the i-th column of the Jacobian. The end-effecter velocity is given by a linear combination of the Jacobian column vectors weighted by the individual joint velocities.

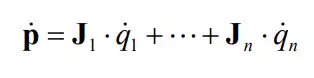
where n is the number of active joints. The geometric interpretation of the column vectors is that is the end-effecter velocity and angular velocity when all the joints other than joint i are immobilized and only the i-th joint is moving at a unit velocity.

Consider the two-dof articulated robot again. This time we use “absolute” joint angles measured from the positive x-axis, as shown in Figure 5.2.2. Note that angle θ 2 is measured from the fixed frame, i.e. the x-axis, rather than a relative frame, e.g. link 1. Obtain the 2-by-2 Jacobian and illustrate the two column vectors on the xy plane. Discuss the result in comparison with the previous case.

Absolute joint angles measured from the x-axis.

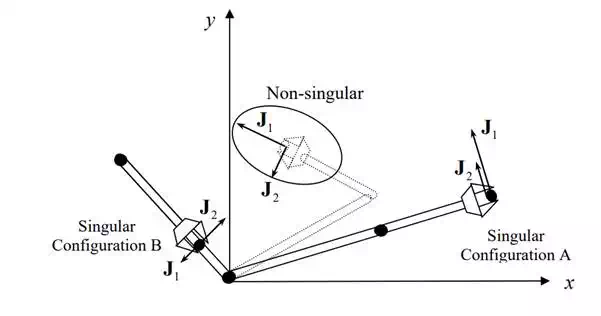
Note that the elements of the Jacobian are functions of joint displacements, and thereby vary with the arm configuration. As expressed in eq.(5.1.8), the partial derivatives, e i e i ∂x / ∂θ , ∂y / ∂θ , are functions of 1 2 θ and θ . Therefore, the column vectors 1 2 vary depending on the arm posture. Remember that the end-effecter velocity is given by the linear combination of the Jacobian column vectors 1 2 . Therefore, the resultant end-effecter velocity varies depending on the direction and magnitude of the Jacobian column vectors 1 2 spanning the two-dimensional space. If the two vectors point in different directions, the whole two-dimensional space is covered with the linear combination of the two vectors. That is, the end effecter can be moved in an arbitrary direction with an arbitrary velocity. If, on the other hand, the two Jacobian column vectors are aligned, the end-effecter cannot be moved in an arbitrary direction. this may happen for particular arm postures where the two links are fully contracted or extended. These arm configurations are referred to as singular configurations. Accordingly, the Jacobian matrix becomes singular at these positions. Using the determinant of a matrix, this condition is expressed as

det J = 0

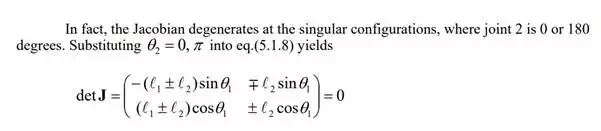
Note that both column vectors point in the same direction and thereby the determinant becomes zero.

Singular configurations of the two-dof articulated robot