Differential Motion

In the previous chapter, the position and orientation of the manipulator end-effecter were evaluated in relation to joint displacements. The joint displacements corresponding to a given end-effecter location were obtained by solving the kinematic equation for the manipulator. This preliminary analysis permitted the robotic system to place the end-effecter at a specified location in space. In this chapter, we are concerned not only with the final location of the end-effecter, but also with the velocity at which the end-effecter moves. In order to move the end-effecter in a specified direction at a specified speed, it is necessary to coordinate the motion of the individual joints. The focus of this chapter is the development of fundamental methods for achieving such coordinated motion in multiple-joint robotic systems. As discussed in the previous chapter, the end-effecter position and orientation are directly related to the joint displacements. Hence, in order to coordinate joint motions, we derive the differential relationship between the joint displacements and the end-effecter location, and then solve for the individual joint motions.

Differential Relationship

We begin by considering a two degree-of-freedom planar robot arm. The kinematic equations relating the end-effecter coordinates and to the joint displacements e x ye θ1 and θ 2 are given by

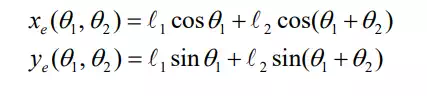
Two dof planar robot with two revolute joints

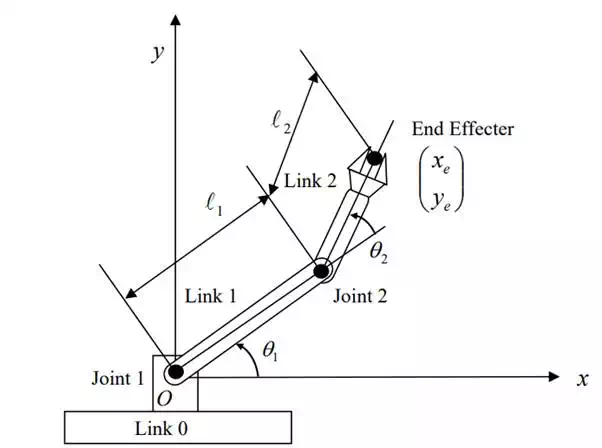
We are concerned with “small movements” of the individual joints at the current position, and we want to know the resultant motion of the end-effecter. This can be obtained by the total derivatives of the above kinematic equations:

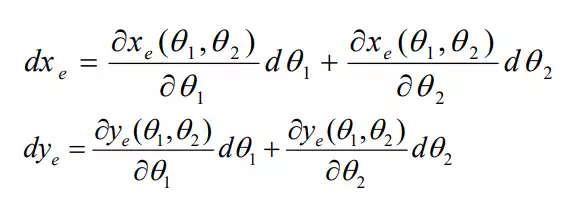
where are variables of both e e x , y θ1 and θ2 , hence two partial derivatives are involved in the total derivatives. In vector form the above equations reduce to

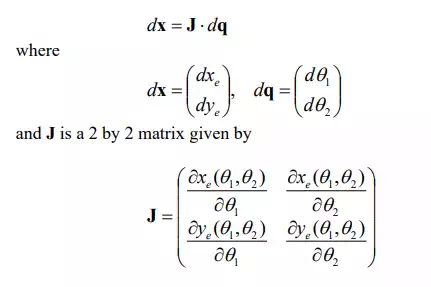
The matrix J comprises the partial derivatives of the functions 1 2 (θ ,θ ) e and 1 2 x (θ ,θ ) e with respect to joint displacements 1 2 y θ and θ . The matrix J, called the Jacobian Matrix, represents the differential relationship between the joint displacements and the resulting end-effecter motion. Note that most robot mechanisms have a multitude of active joints, hence a matrix is needed for describing the mapping of the vectorial joint motion to the vectorial end-effecter motion.

 For the two-dof robot arm of, the components of the Jacobian matrix are computed as

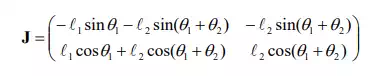
By definition, the Jacobian collectively represents the sensitivities of individual end-effecter coordinates to individual joint displacements. This sensitivity information is needed in order to coordinate the multi dof joint displacements for generating a desired motion at the end-effecter.

Thus the Jacobian determines the velocity relationship between the joints and the end-effecter.