Kinematics of Parallel Link Mechanisms

Consider the five-bar-link planar robot arm

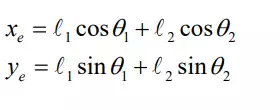
Note that Joint 2 is a passive joint. Hence, angle θ2 is a dependent variable. Using θ2 , however, we can obtain the coordinates of point A:

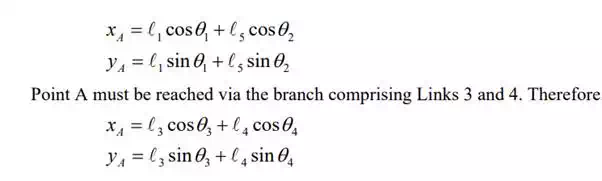
Equating these two sets of equations yields two constraint equations:

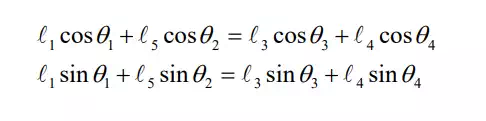
Note that there are four variables and two constraint equations. Therefore, two of the variables, such as  θ1 ,θ2 , are independent. It should also be noted that multiple solutions exist for these constraint equations.

Five-bar-link mechanism

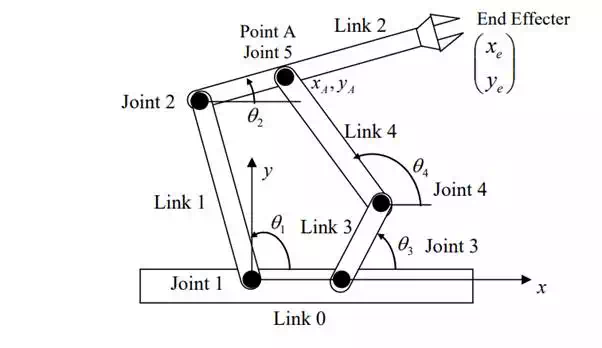
Although the forward kinematic equations are difficult to write out explicitly, the inverse kinematic equations can be obtained for this parallel link mechanism. The problem is to find 1 3 θ ,θ that lead the endpoint to a desired position: . We will take the following procedure:

Step 1 Given , find e e x , y 1 2 θ ,θ by solving the two-link inverse kinematics problem.

Step 2 Given 1 2 θ ,θ , obtain . This is a forward kinematics problem. A A x , y

Step 3 Given , find A A x , y 3 4 θ ,θ by solving another two-link inverse kinematics problem.

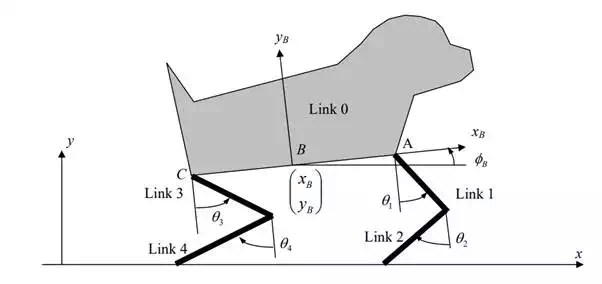
Obtain the joint angles of the dog’s legs, given the body position and orientation.

A doggy robot with two legs on the ground

Redundant mechanisms

A manipulator arm must have at least six degrees of freedom in order to locate its end effecter at an arbitrary point with an arbitrary orientation in space. Manipulator arms with less than 6 degrees of freedom are not able to perform such arbitrary positioning. On the other hand, if a manipulator arm has more than 6 degrees of freedom, there exist an infinite number of solutions to the kinematic equation. Consider for example the human arm, which has seven degrees of freedom, excluding the joints at the fingers. Even if the hand is fixed on a table, one can change the elbow position continuously without changing the hand location. This implies that there exist an infinite set of joint displacements that lead the hand to the same location. Manipulator arms with more than six degrees of freedom are referred to as redundant manipulators. We will discuss redundant manipulators in detail in the following chapter.