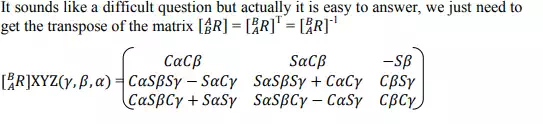Position, Orientation, Frames

Introduction

In this section I will try to summarize how to define position coordinate on the space with respect to the origin frame and to calculate the transformation when this frame rotates with respect to the base frame.

There is frame A and frame B.

Frame B rotates with respect to frame A

1. Find rotation B in A?

2. Find the coordinate ? The coordinate of p (0 3 1) The coordinate of pB (0 1 1)

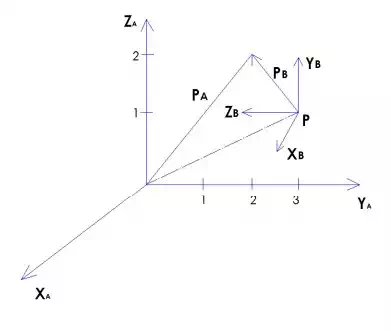
Frame B rotate with respect to frame A

Now we need to find the translation.

We add extra row which represents rotation axis (0 0 0 1), then we make dot product between rotation matrix and the coordinate of pB (0 1 1) and then we get the coordinate of PA (Tapani Kuusi, lecture on Lahti University of Applied Sciences 2010).

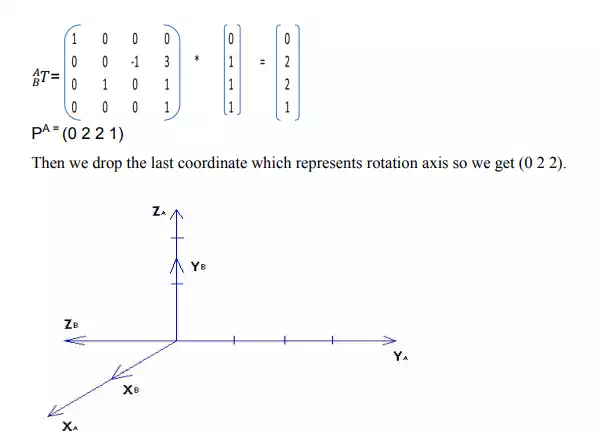
Example 2:

There is rotation from P to P2 around X axis

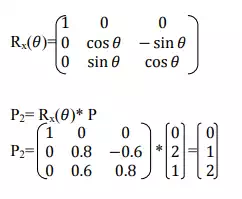
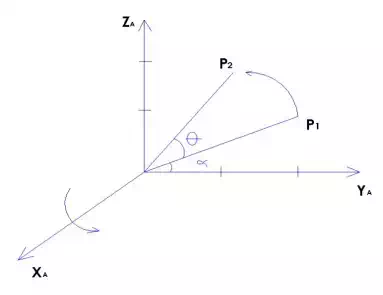
Rotation around X axis

Example

In the following example frame B rotates with respect to frame A.

We have 3 different rotations.

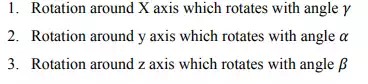
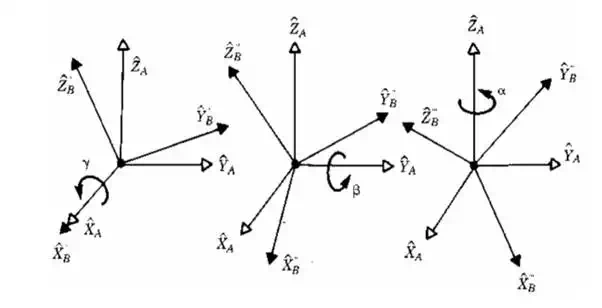
Rotation axes

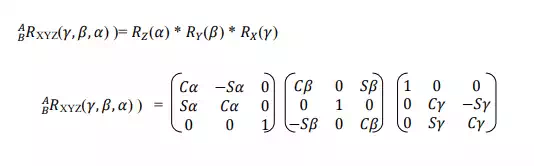
Important Notice: How we can make the calculation for B rotating around A?